Hypothesis testing and confidence Interval are inferential techniques that use an approximation of sample distribution. Confidence intervals use sample data to estimate a population parameter. Whereas, hypothesis testing uses sample data to test a hypothesis.
In this article, we will discuss what is confidence interval with examples and will implement this using Python.
Table of Contents
ToggleWhat is Confidence Interval (CI)?
There is always some uncertainty when we estimate a value using sample data instead of population data.
The confidence interval gives a range of values where our estimate lies with a confidence level.
CI = Estimate Mean ± Variation in Estimation
Example
Statement:
What is the manufacturing part diameter on Machine A with a confidence level of 95%?
Solution:
Using CI, with a 95% confidence level we can conclude the following:
- The manufactured part diameter is between 10 and 11 mm using sample data from the population.
Inference from solution considering 95% confidence level:
- If we pick 100 samples from a population, 95 times the part diameter will be 10 to 11 mm.
- In 95 samples out of 100, all parts diameter will vary from 10mm to 11 mm.
Confidence level = 1- Significance Level
Application Example of Confidence Intervals
We use CI to determine variation around a point estimate.
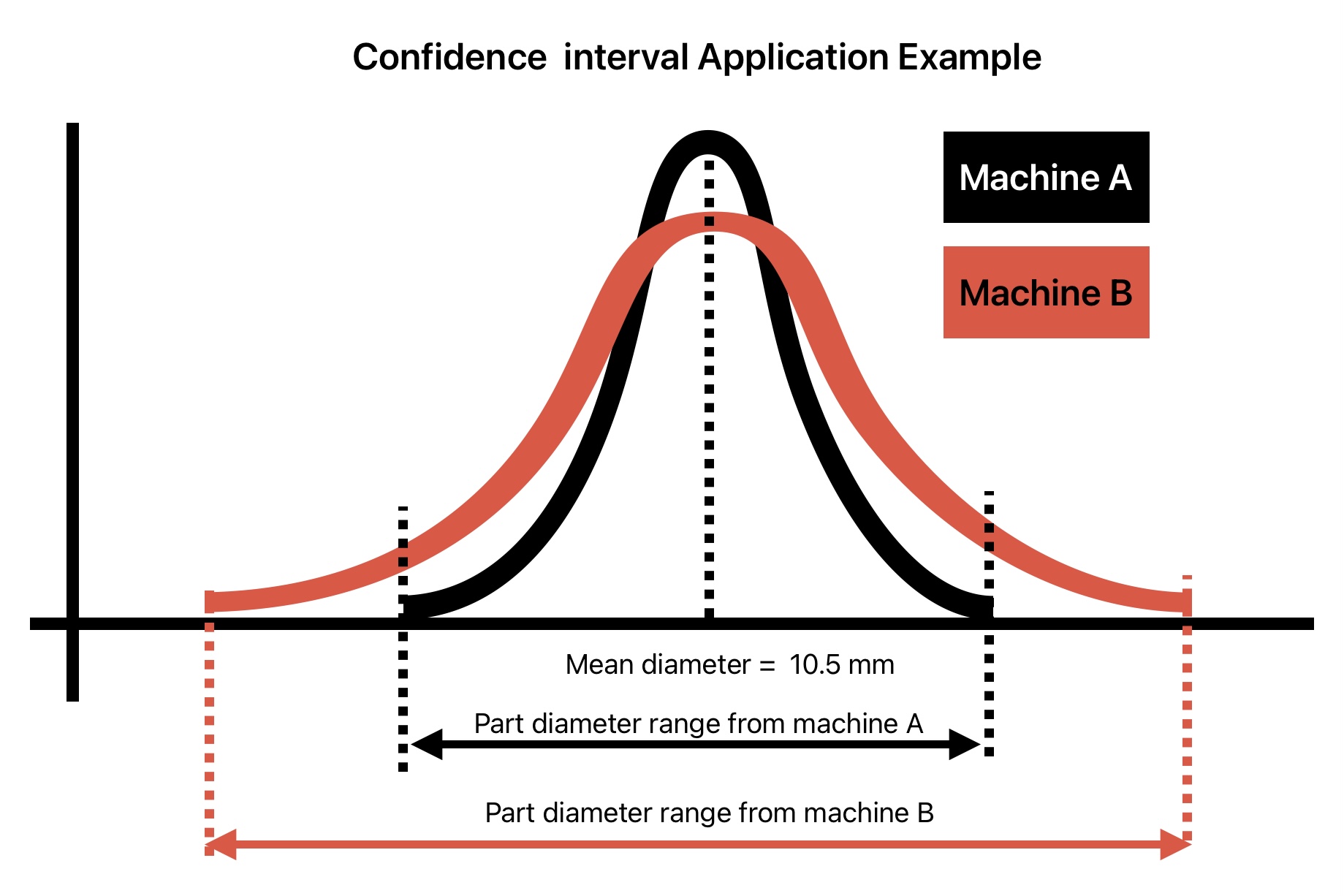
We should use confidence interval instead of average because of the following possibility.
- The average manufactured part diameter from both machines is 10.5mm.
- However, the variation in part diameter between the two machines is different. In other words, both machines have different process capabilities.
Confidence Interval Calculation
We require the following inputs to calculate the CI:
- Sample Size
- Sample standard deviation.
- The point estimate (Sample mean, variation between two groups, difference in sample mean)
- Critical values for the test statistic
Confidence Interval Formula

- The CI tells us the number of standard deviations data is away from the mean.
- We need to reach the required confidence level to get the desired CI.
- We can use z-test or t-test to calculate the critical values.
Representation of CI
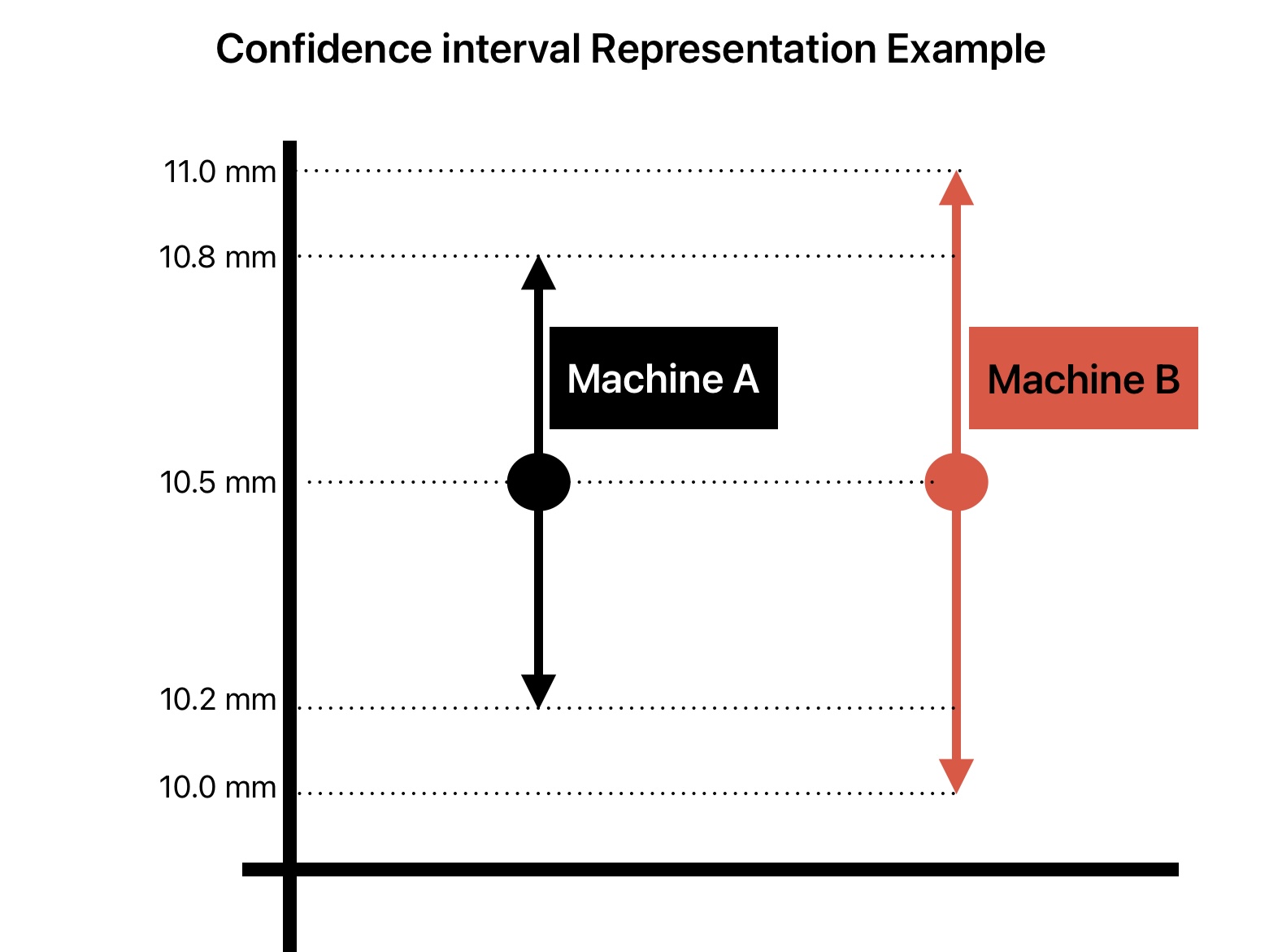
As shown in the above image, we can represent CI by showing a range where the values can vary.
Confidence Interval Implementation Example in Python
A sample individual part weight is measured on the production line randomly. Find the confidence interval for the mean weight of the part with 95% confidence level.
Import the required Library, get the Data, and define confidence level
# Import Required Library
import numpy as np
from scipy import stats
# Get the sample Data
sample_part_weight = [15, 15.01, 15.1, 14.9, 14.95, 15, 15.15, 15.01, 15, 14.8, 14.9, 14.95,
15.12, 14.95, 15, 14.95, 15.02, 15.01, 15.1, 15.05, 15.1, 15, 15.15, 15,
15.01, 15.1, 15.15, 15, 15.15]# Define the confidence Level
cl = 0.95Calculate the mean and standard error of the mean (SEM)
mean_value = np.mean(sample_part_weight)
sem_value = stats.sem(sample_part_weight)Calculate the confidence interval
confidence_interval = stats.t.interval(cl, len(sample_part_weight) - 1, loc=mean_value, scale=sem_value)
print(confidence_interval)(14.989255203811918, 15.05419307205015)
Results Interpretations
print("Sample Mean:", mean_value)
print("Standard Error of the Mean:", sem_value)
print(f"{cl * 100:.2f}% Confidence Interval:", confidence_interval)Sample Mean: 15.021724137931034 Standard Error of the Mean: 0.015850820599394765 95.00% Confidence Interval: (14.989255203811918, 15.05419307205015)
Conclusion
This article covers the importance of confidence interval in statistics and steps to calculate the confidence interval. To sum up, CI determines the limits or a range of values where our estimate lie with a given confidence level.
If you have any doubts or questions, please let us know in the comment section!
