We use machine learning to solve complex problems using lots of input or training data. For this, we build and train our machine learning algorithms. But how can we ensure our ML model is meeting our expectations? Machine Learning model evaluation is a critical step during ML project development. It ensures our ML Model is generalizing on unseen data.
Table of Contents
ToggleMachine Learning Model Evaluation Metrics
Multiple machine learning model evaluation metrics are available. Each evaluation metric has its importance and applications. The selection of wrong evaluation metrics can lead to unsatisfactory results.
Sometimes ML model gives satisfactory results on accuracy score. But poor results on other machine learning model evaluation matrices. Here is the list of Evaluation metrics we can use to determine the performance of Machine Learning Algorithms.
Classification Machine Learning Model Evaluation Metrics
Here is the list of techniques, we can use to evaluate classification machine learning algorithms.
- Accuracy
- False Positive and False Negative
- Precision and Recall
- Logarithmic Loss
- Confusion Matrix
- F1 Score
- ROC Curve
- Area Under the Curve
Terminologies in Classification Evaluation Metrics
We need to understand the following four terms to understand machine learning evaluation metrics for classification tasks.
- True Positive
- True Negative
- False Positive
- False Negative
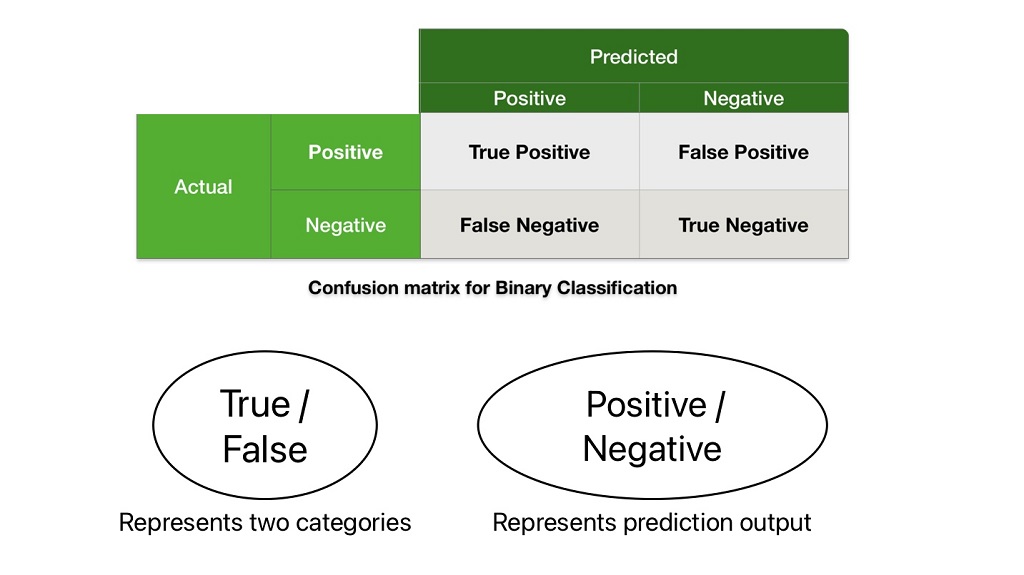
The above four terms have two characters: True/false and Positive/ Negative.
Here, positive and negative characters represent two categories that can be spam or not spam, cat or Dog. We can consider any of these categories positive or negative. It has nothing to do with positive or negative nature.
True/false represents the prediction output. True indicates the ML algorithm predicting the given class correctly. Whereas false indicates the ML algorithm is not predicting the given class correctly.
Let’s try to understand these terms considering the example of the classification of a cat or Dog. We will consider cats as a positive class and dogs as a negative class.
1. True Positive
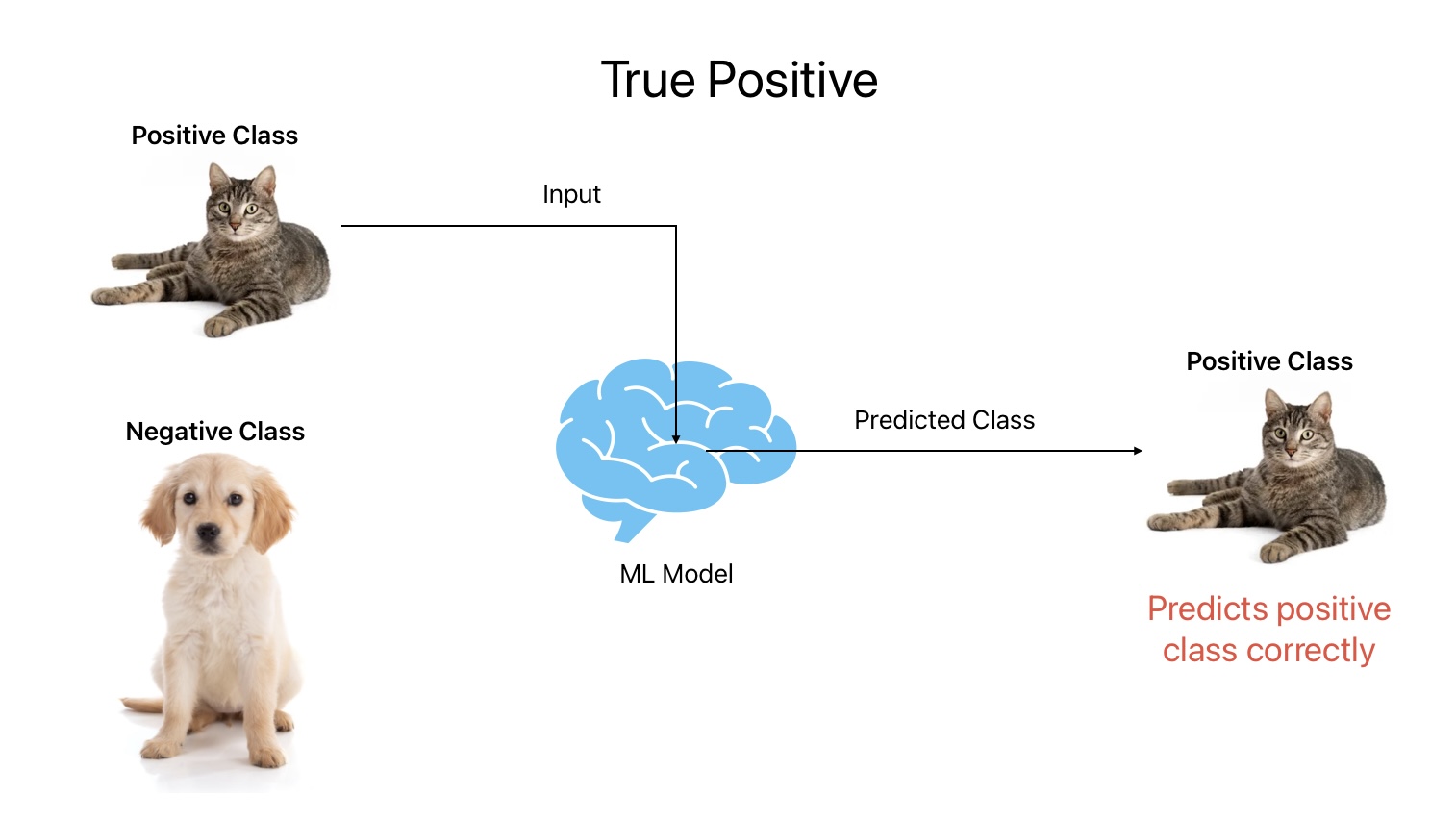
True Positive is an outcome where the ML model predicts positive class correctly. In other words, the ML model predicts Cat as Cat.
2. True Negative
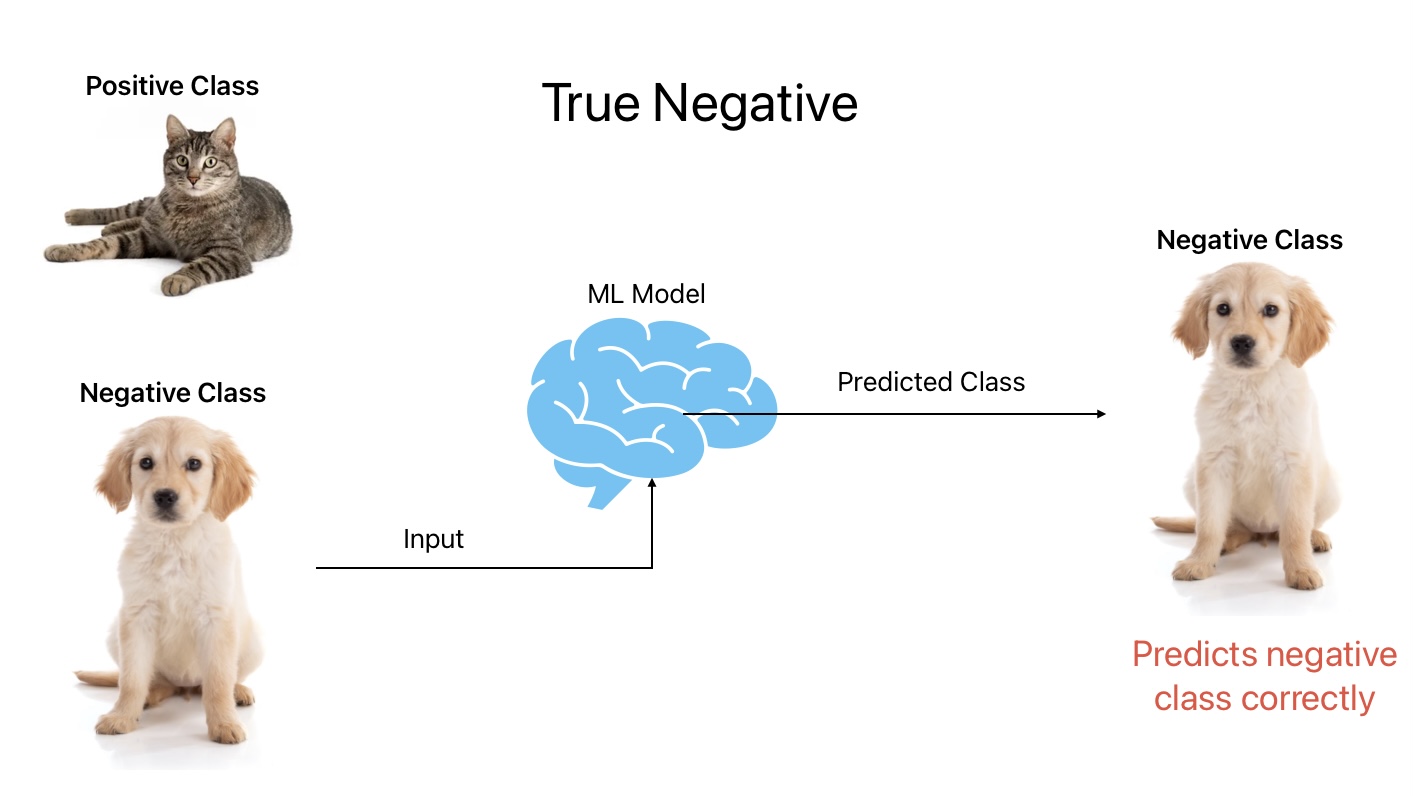
True Negative is an outcome where the ML model predicts a negative class correctly. In other words, the ML model predicts dogs as dogs.
3. False Positive
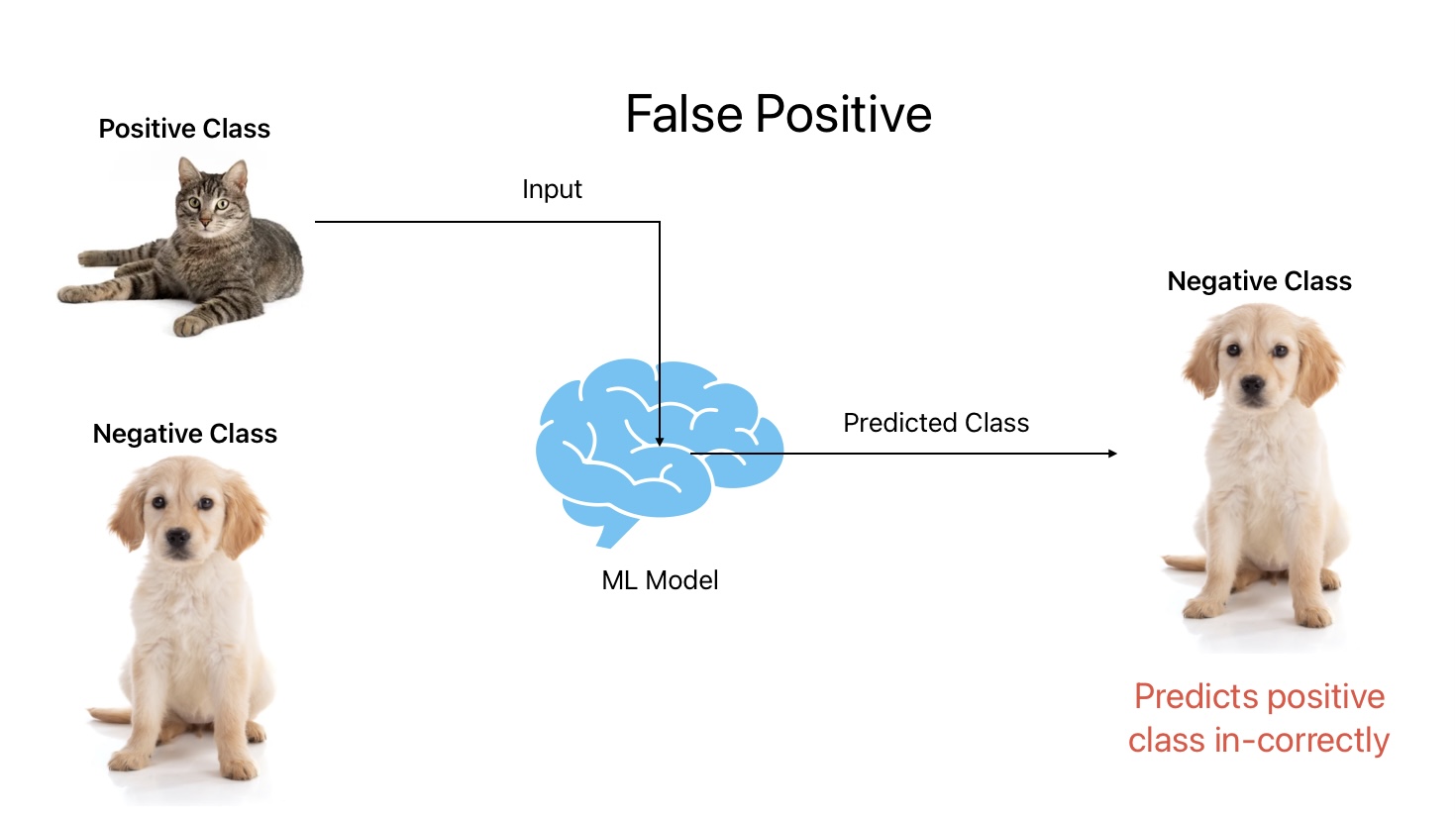
False Positive is an outcome where the ML model predicts a positive class correctly. In other words, the ML model predicts a cat as a dog.
4. False Negative
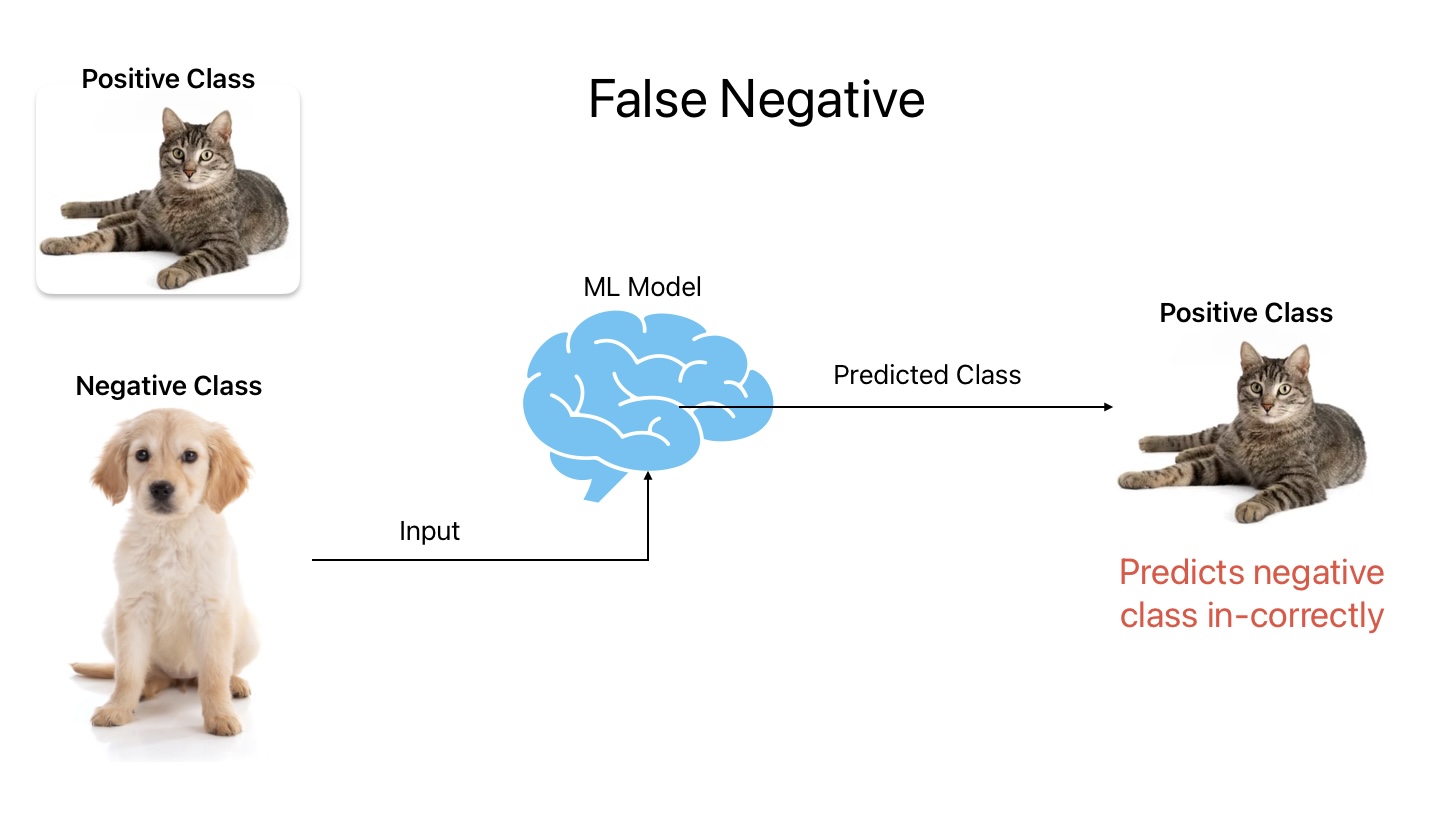
False Negative is an outcome where the ML model predicts negative class in-correctly. In other words, the ML model predicts dogs as cats.
Confusion Matrix
It measures performance for classification problems where the output can be two or more classes. Confusion Matrix is a graphical representation that gives an idea about model performance.
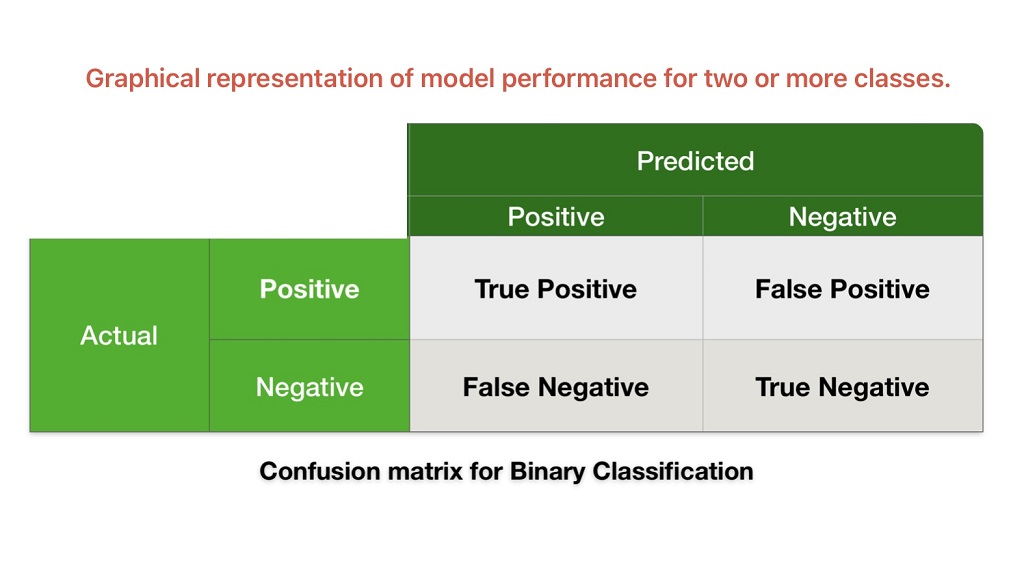
We can use this machine learning algorithm evaluation metrics to calculate accuracy, precision, recall, and AUC-ROC Curve.
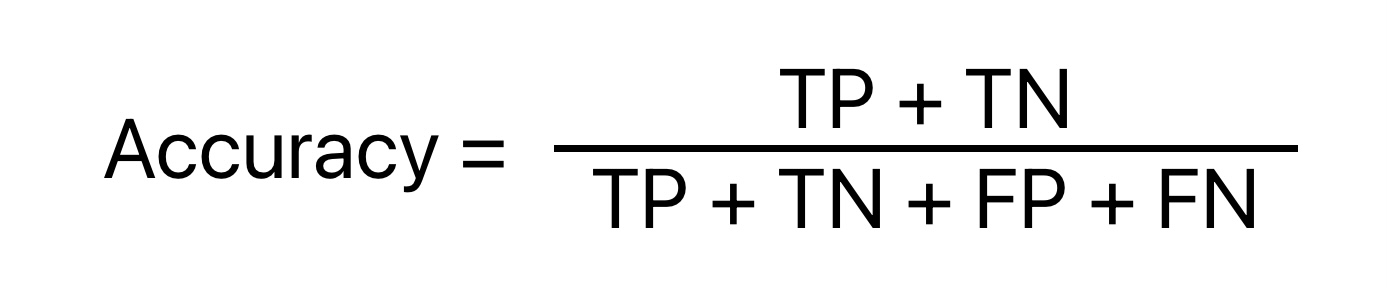
Accuracy
Mathematically, accuracy is the ratio of the number of correct predictions and the total number of predictions.
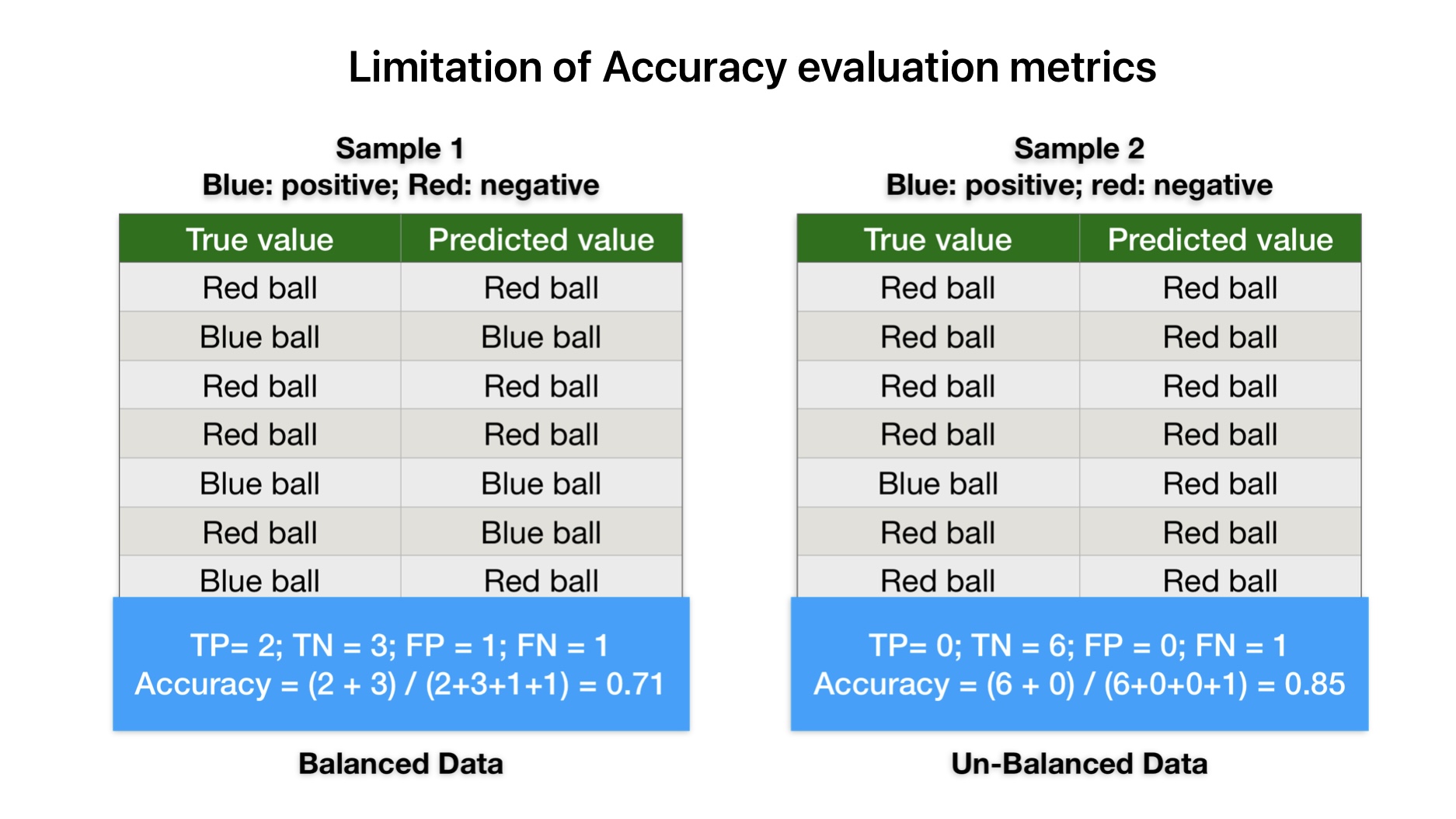
Accuracy is not an accurate measure of performance for unbalanced data. For example, in sample-2 data, the ML model predicts all values as red balls irrespective of their color. But accuracy results are still looking impressive. Therefore accuracy is not a good measure of machine learning model evaluation metrics.
Precision: Machine Learning Model Evaluation Metrics
Mathematically, Precision is the ratio of True Positive and the total number of instances classified as positive in the data. Its values vary from 0 to 1 (1 being best and 0 being worst).
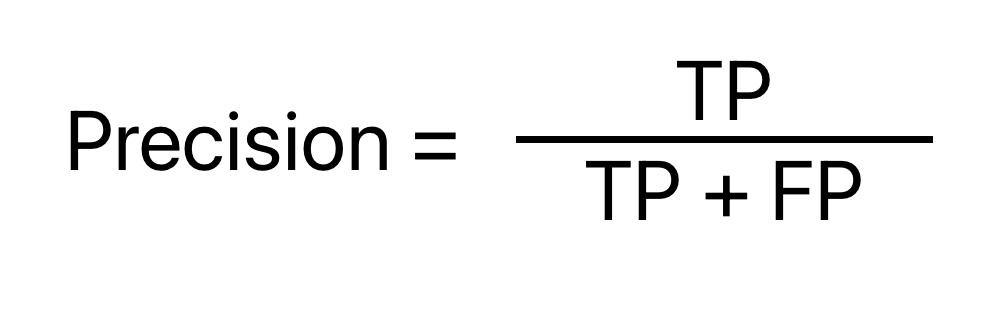
Precision machine learning model evaluation metrics has nothing to do with total data points or negative instances. In other words, precision does not tell anything about False Negative (the number of positive class predictions are wrongly classified)
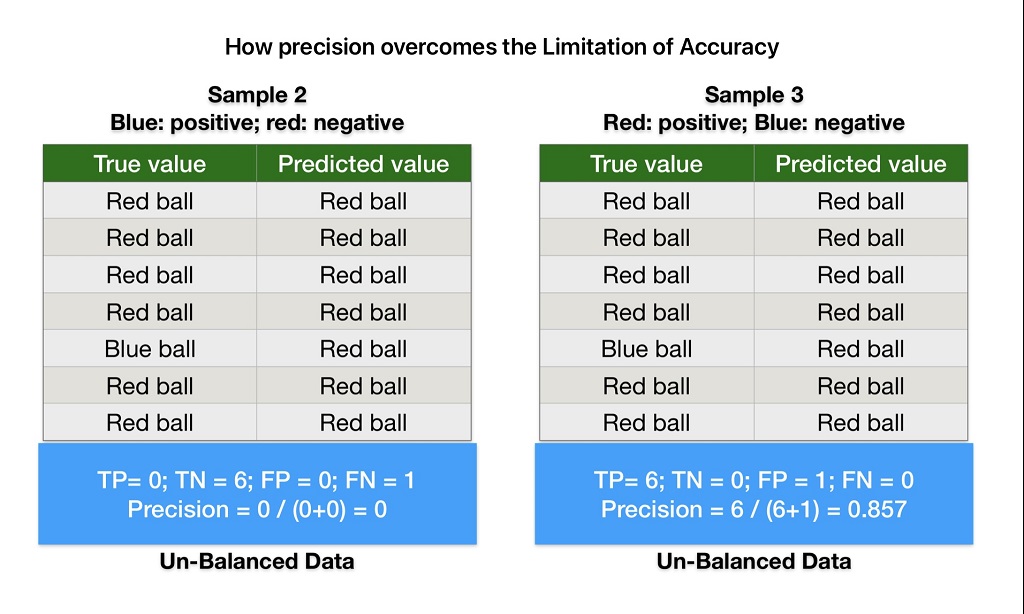
Accuracy is not an accurate measure of performance for unbalanced data. For example, our ML model predicts all balls red balls irrespective of their color in sample-2. But accuracy results are still looking impressive.
But precision equal to 0 indicates our model needs improvement. Therefore we can use precision machine learning model evaluation metrics to overcome accuracy limitations.
Recall or Sensitivity
Mathematically recall or sensitivity is the ratio of True Positive and the total number of positive instances in the data. It has nothing to do with the number of total data points or negative instances.
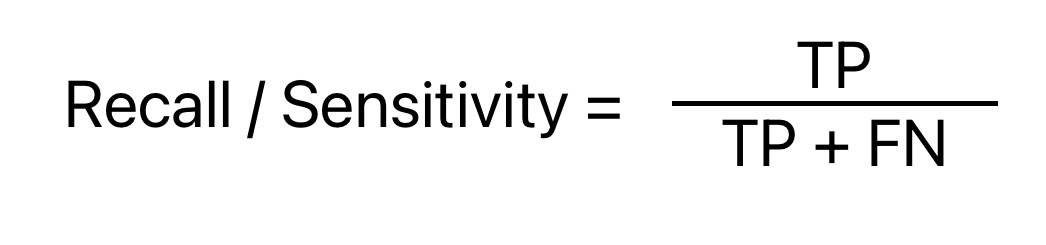
Recall is similar to precision, but it calculates the percentage of actual positives that the machine learning model has identified incorrectly.
Precision vs Recall
Both precision and recall machine learning model evaluation metrics look similar, but they are different and inversely proportional. An increase in recall will result in a decrease in precision.
But the question is how to select the best machine learning algorithm evaluation metrics between precision and accuracy.
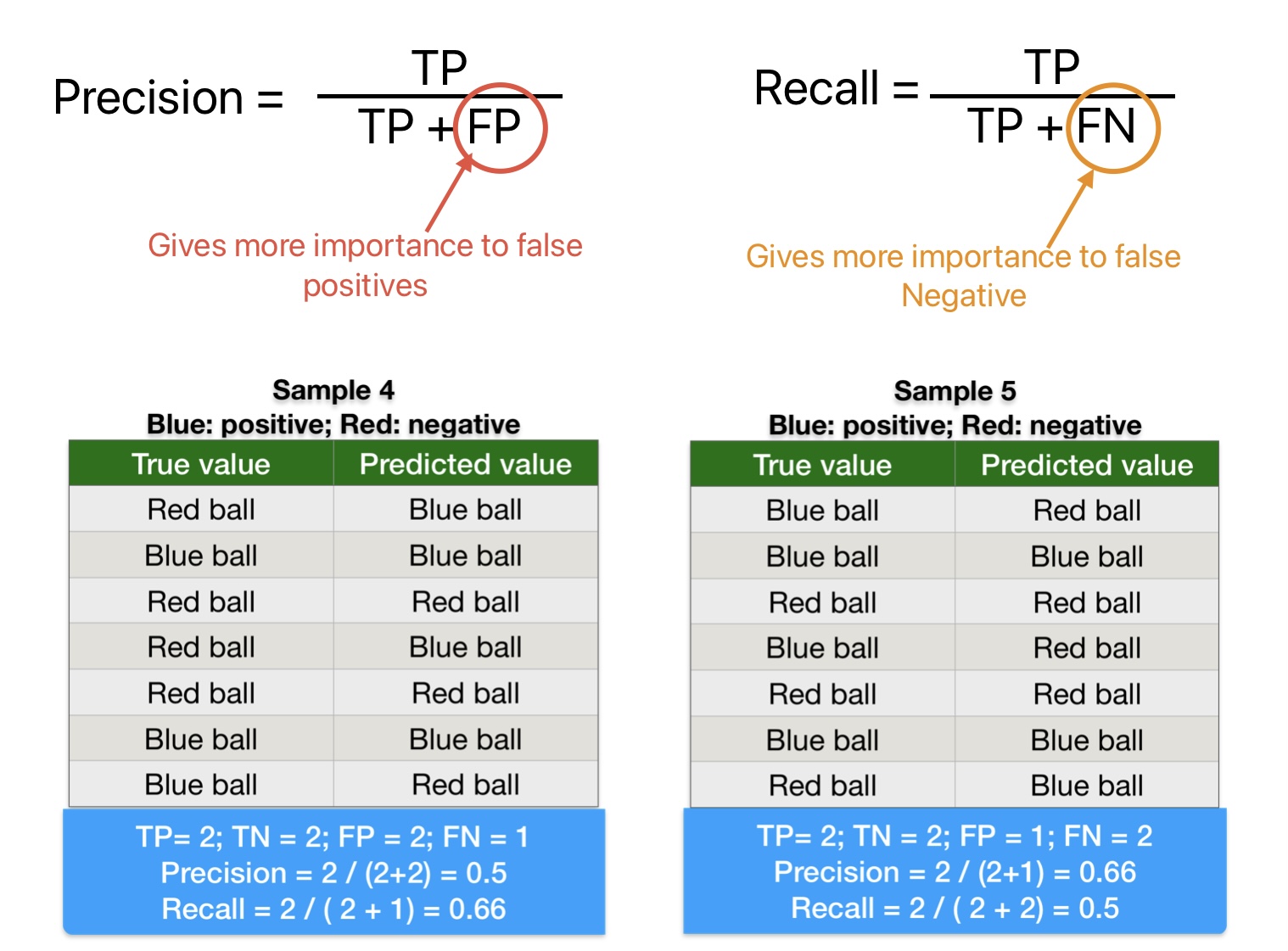
A comparison of the above precision and recall calculation formula indicates the following points:
- Precision gives more importance to False Positive. (Positive instances classified as negative).
- Recall gives more importance to False Negative. (Negative instances classified as positives).
Therefore, experts recommend Precision evaluation metrics if we don’t want False Positive predictions and recall if we don’t want false negative predictions.
Let’s consider a case where we are predicting whether a patient has cancer (Positive) or does not have Cancer (Negative). Our goal is to detect all cancer patients. As a result, we don’t want False Positives in our prediction. Therefore, Precision is the right machine learning model evaluation metrics here.
In another case, we are predicting whether an email is spam (Positive) or not spam (Negative). Our goal is not to classify important emails as spam. It’s OK if our user has some spam in their inbox. In other words, we don’t want False Negative (predicting not-spam as spam) in our prediction. Therefore Recall or Sensitivity is the right machine learning model evaluation metrics for this application.
F-Score/F1 Score
Mathematically, F1 Score is the harmonic mean of Precision and Recall.
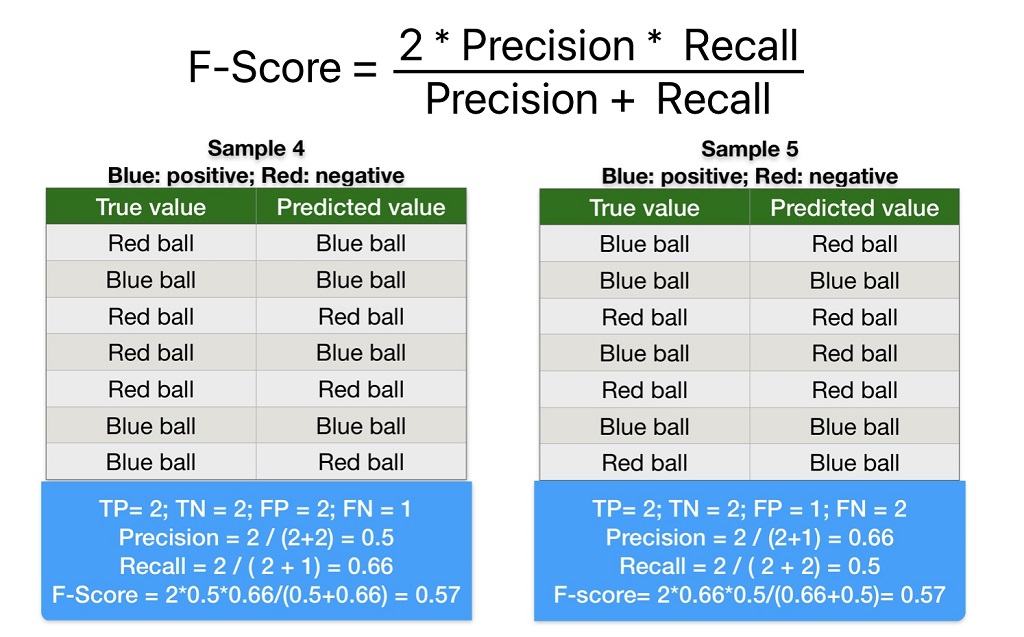
We can use the F1 Score evaluation metrics for Binary Classification problems. It gives equal weight to both precision and recall. Therefore, experts recommend the F-Score evaluation metrics in machine learning models where both False Positive and False Negative are important, and the positive class has few observations.
AUC - ROC Curve: Machine Learning Model Evaluation Metrics
We can use the AUC(Area under Curve)-ROC(Receiver Operating Characteristic) curve to evaluate binary and multi-class classification model performance on the graph.
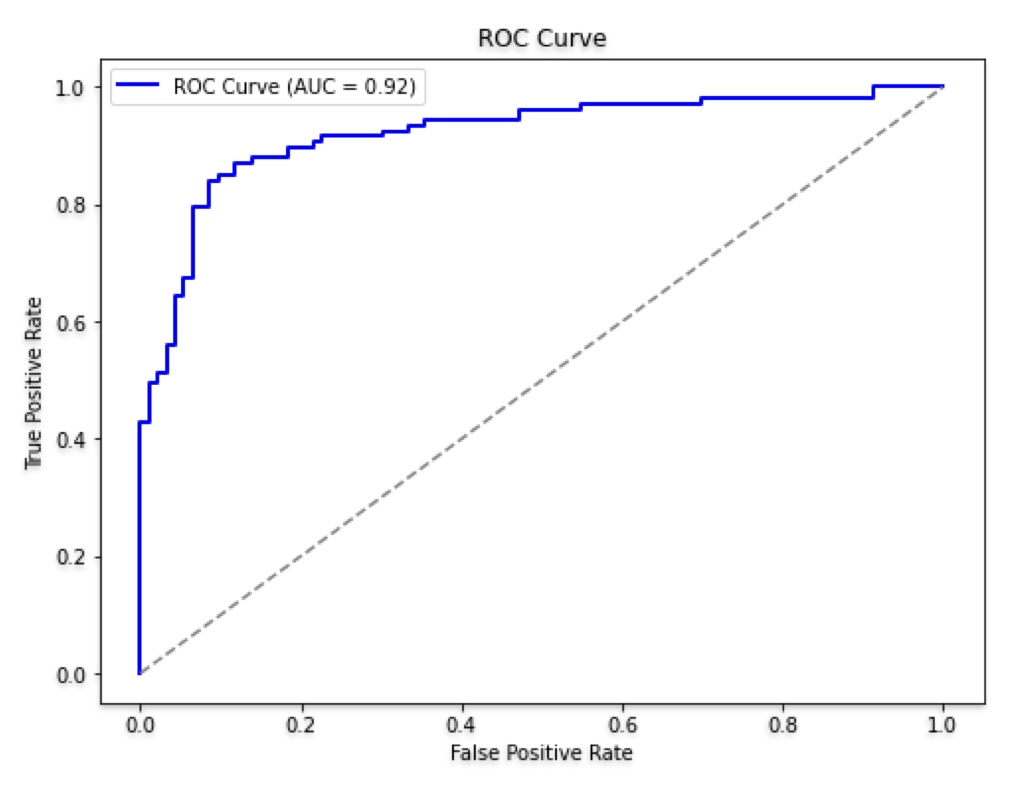
ROC is a Probability curve, whereas AUC represents the degree of separability. The Higher the value of AUC (AUC = 1), the better will be the model’s ability to classify two categories. AUC gives aggregate measures of performance across all possible classification thresholds.
The ROC Curve is a graph between the True Positive Rate (X-axis) and False Positive Rate (y-axis). It shows the performance of the classification model at different thresholds.

True Positive Rate (TPR): Percentage of all positive observations that were correctly expected to be positive.
False Positive Rate (FPR): Fraction of negative observations that are mistakenly projected to be positive.
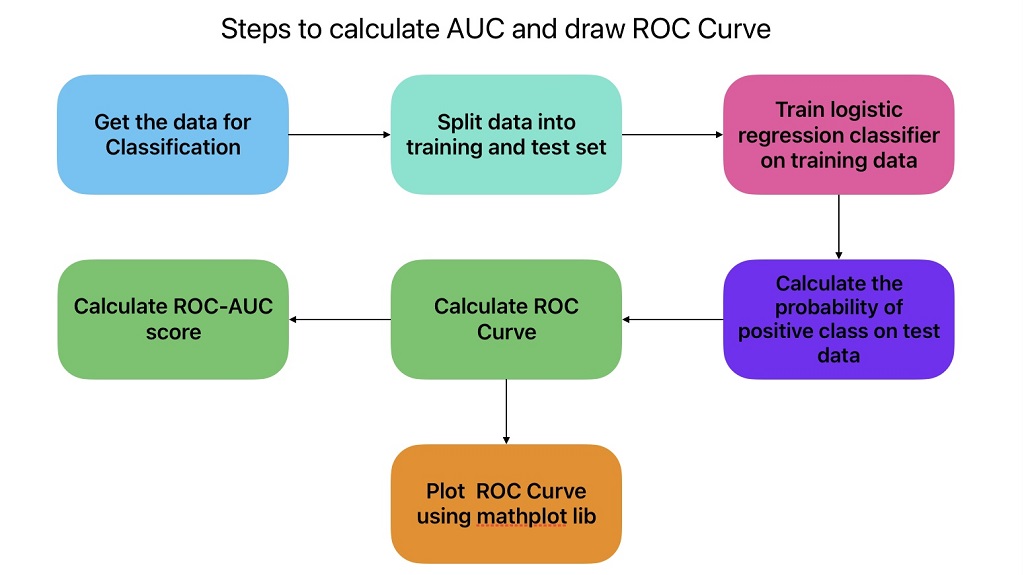
To get the points for the ROC curve, we need to evaluate the classification model many times with different classification thresholds.
Regression Machine Learning Model Evaluation Metrics
Here is the list of techniques, we can use to evaluate regression machine learning algorithms.
- Mean Absolute Error
- Mean Squared Error
- Root Mean Squared Error
- Mean Absolute Percentage Error
Mean Absolute Error (MAE): ML Model Evaluation
Mean Absolute error is the arithmetical mean of the absolute error.
- Absolute error is the mode of the difference between the predicted value and the actual value.
- MAE error unit is same as the predicted variable.
Formula for Mean Absolute Error
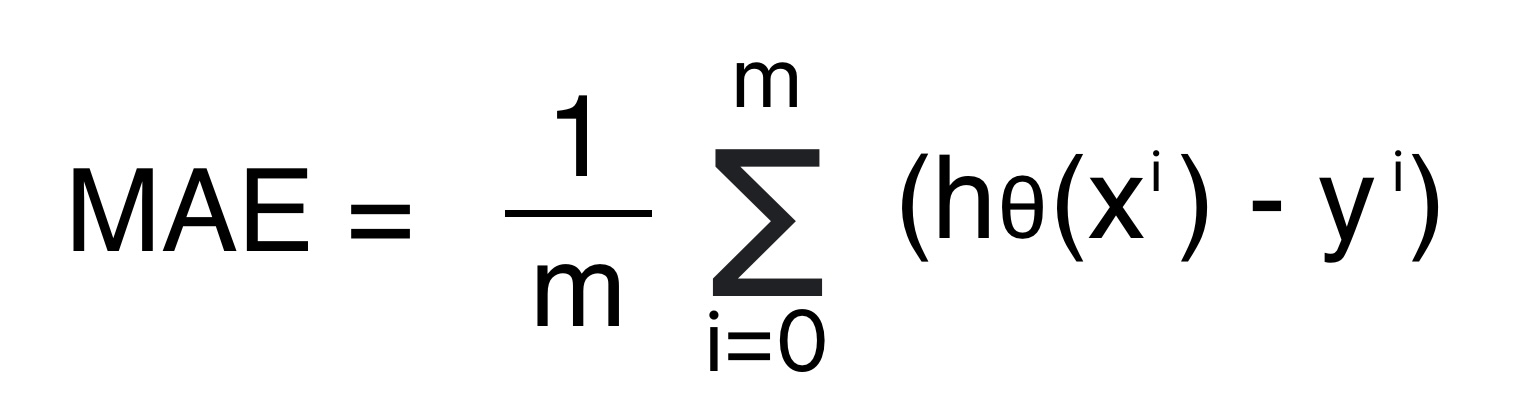
Mean Absolute Error Calculation Example
The below image shows multiple datasets with the following characteristics:
- Simple Data
- Data with outliner
- Increased scale
- Negative error.
Here we calculated the mean absolute error using manual calculations. We recommend you use this data to get hands-on MAE calculations manually and using Python.
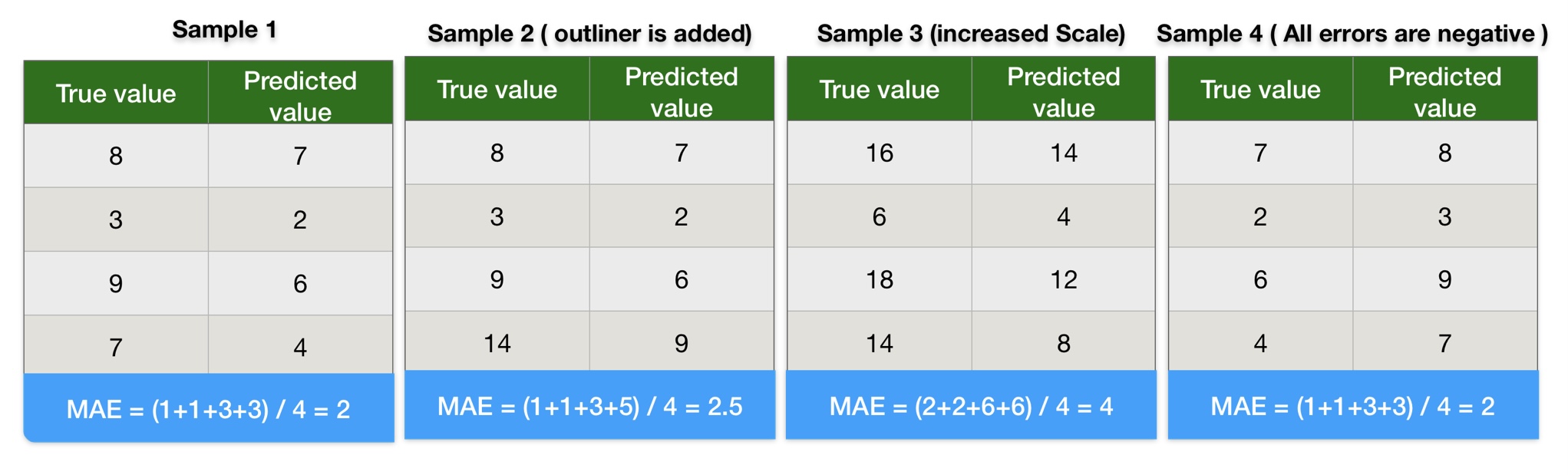
We can conclude the following points from the results of mean absolute error calculation results:
- Results of MAE in sample-1 and sample-2 indicate outliners do not impact mean absolute error.
- MAE values in sample-1 and sample-3 indicate an increase in the scale of data and also increase the mean absolute error on the same scale. In other words, the MAE score is linear. The higher the scale of error, the higher the MAE score. Therefore, the MAE score gives a clear picture of the error scale.
- Results of MAE in sample-1 and sample-4 indicate a negative error does not impact mean absolute error.
Python Code to Calculate the Mean Absolute Error
# import required Library
import pandas as pd
import numpy as np# Create Sample-1 Dataframe
sample1 = {
'true_value': [8, 3, 9, 7],
'predicted_value': [7, 2, 6, 4]
}
sample1_df = pd.DataFrame(sample1)
# Create Sample-2 Dataframe
sample2 = {
'true_value': [8, 3, 9, 14],
'predicted_value': [7, 2, 6, 9]
}
sample2_df = pd.DataFrame(sample2)
# Crete Sample-3 Dataframe
sample3 = {
'true_value': [16, 6, 18, 14],
'predicted_value': [14, 4, 12, 8]
}
sample3_df = pd.DataFrame(sample3)
# Crete Sample-4 Dataframe
sample4 = {
'true_value': [7, 2, 6, 4],
'predicted_value': [8, 3, 9, 7]
}
sample4_df = pd.DataFrame(sample4)# Import required library to measure Mean Absolute error
from sklearn.metrics import mean_absolute_error# Calculate Mean Absolute Error
mae_sample1 = mean_absolute_error(sample1_df["true_value"], sample1_df["predicted_value"])
mae_sample2 = mean_absolute_error(sample2_df["true_value"], sample2_df["predicted_value"])
mae_sample3 = mean_absolute_error(sample3_df["true_value"], sample3_df["predicted_value"])
mae_sample4 = mean_absolute_error(sample4_df["true_value"], sample4_df["predicted_value"]) # Print the Data
print("Mean Absolute error for Sample-1 Data is ", mae_sample1)
print("Mean Absolute error for Sample-2 Data is ", mae_sample2)
print("Mean Absolute error for Sample-3 Data is ", mae_sample3)
print("Mean Absolute error for Sample-4 Data is ", mae_sample4)Mean Absolute error for Sample-1 Data is 2.0 Mean Absolute error for Sample-2 Data is 2.5 Mean Absolute error for Sample-3 Data is 4.0 Mean Absolute error for Sample-4 Data is 2.0
Mean Squared Error (MSE): Regression ML Model Evaluation Technique
Mean Squared error is the arithmetical mean of the square of the difference between the predicted value and actual value.
- MSE is always positive since we are squaring the error value.
- Mean squared error is the variance of prediction error.
Formula for Mean Squared error
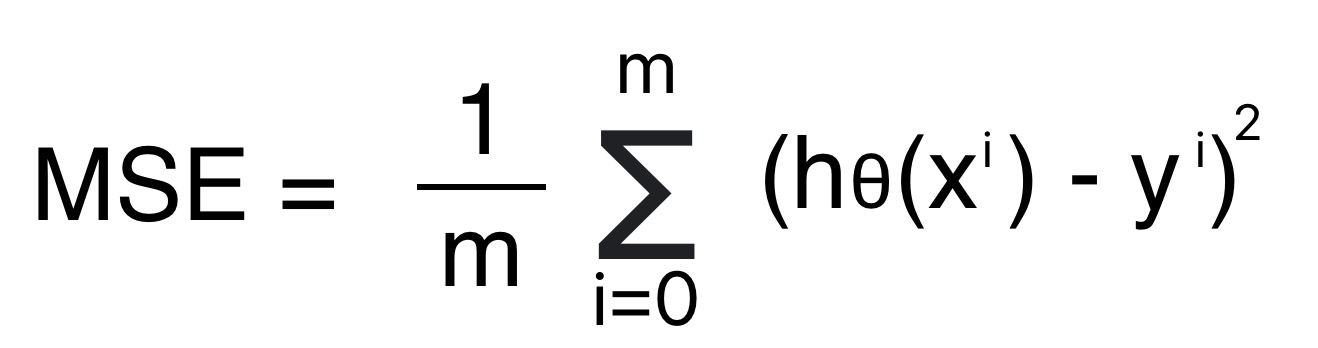
We can conclude the following points on mean square error evaluation metrics.
- Mean square error gives no clue on the direction of inaccuracy.
- The interpretation from MSE is less intuitive because it squares the error. If the error is in minutes MAE will be in squared minutes.
- MSE is always positive. Positive and negative values always sum up. As a result, we will always get the sum of errors as output.
- Squaring error increases the impact of the large errors. As a result, the ML Model penalizes more for large errors.
Mean Square Error Calculation Example
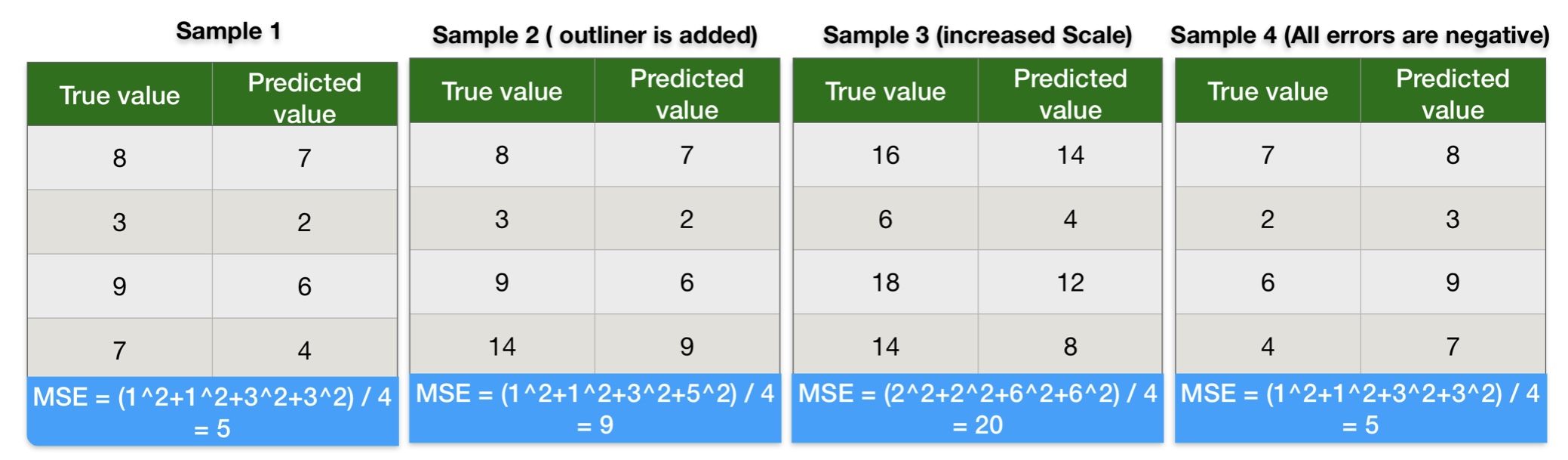
We can conclude the following points from the results of mean square error calculation results:
- Results of MSE in sample-1 and sample-2 indicate mean square error gives more weight to outliners.
- MSE values in sample-1 and sample-3 indicate an increase in the scale of data also increase the mean square error.
- Results of MSE in sample-1 and sample-4 indicate a negative error does not impact mean square error.
Python Code to Calculate the Mean Absolute Error
# Import required library to measure Mean square error
from sklearn.metrics import mean_squared_error# Calculate Mean Square Error
mse_sample1 = mean_squared_error(sample1_df["true_value"], sample1_df["predicted_value"])
mse_sample2 = mean_squared_error(sample2_df["true_value"], sample2_df["predicted_value"])
mse_sample3 = mean_squared_error(sample3_df["true_value"], sample3_df["predicted_value"])
mse_sample4 = mean_squared_error(sample4_df["true_value"], sample4_df["predicted_value"]) print("Mean Squared error for Sample-1 Data is ", mse_sample1)
print("Mean Squared error for Sample-2 Data is ", mse_sample2)
print("Mean Squared error for Sample-3 Data is ", mse_sample3)
print("Mean Squared error for Sample-4 Data is ", mse_sample4)Mean Squared error for Sample-1 Data is 5.0 Mean Squared error for Sample-2 Data is 9.0 Mean Squared error for Sample-3 Data is 20.0 Mean Squared error for Sample-4 Data is 5.0
Root Mean Squared Error: Regression ML Model Evaluation Technique
Root Mean squared error is the square root of the arithmetical mean of the square of the difference between predicted and actual value. We can also calculate RMSE by calculating the square root of the mean squared error.
Root Mean Squared error is the standard deviation of prediction error. It indicates how far the predicted value is from the actual value using Euclidean distance.
Formula for Root Mean Squared Error
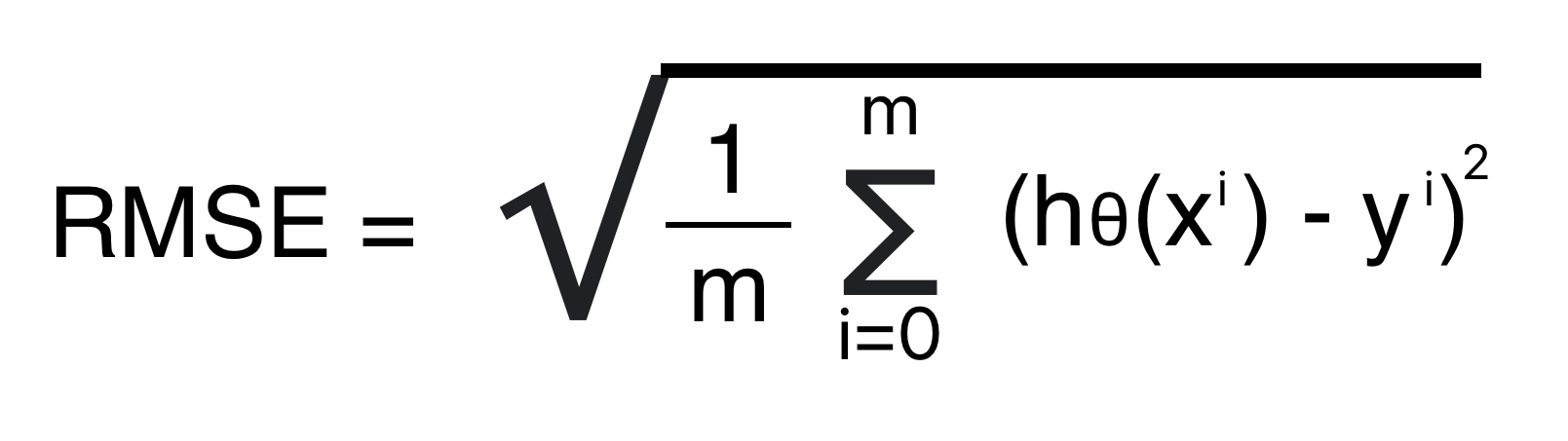
- Provides no clue on the direction of inaccuracy.
- RMSE is a single parameter that can evaluate a model’s performance.
- The interpretation from RMSE is more intuitive because its units are the same as the units of measurement parameter.
- RMSE is always positive. Positive and negative error values always sum up. As a result, we will always get a sum of errors in output.
Root Mean Square Error Calculation Example
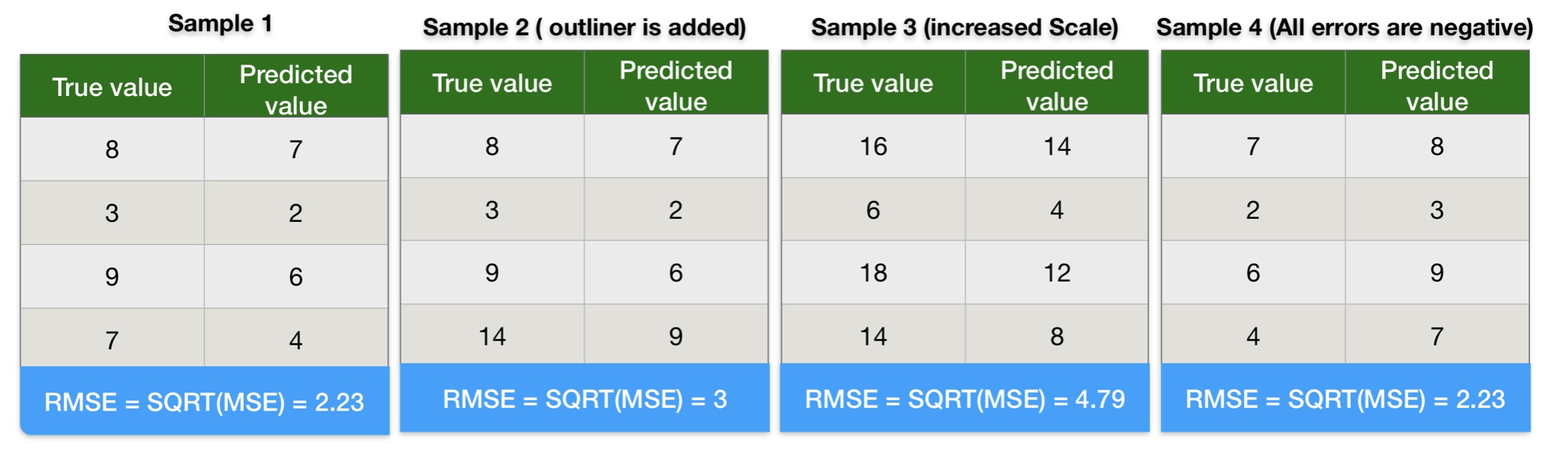
We can conclude the following points from the root mean square error calculation results:
- Results of RMSE in sample-1 and sample-2 indicate root mean square error gives more weight to outliners.
- RMSE values in sample-1 and sample-3 indicate squaring error increases the impact of huge errors. As a result, the ML Model penalizes more if the error is large.
- Results of RMSE in sample-1 and sample-4 indicate a negative error does not impact root mean square error.
Python Code to Calculate Root Mean Square Error
# There is no direct library to calculate root mean square error in sklearn. We can calculate it by doing squareroot of mse.
rmse_sample1 = np.sqrt(mse_sample1)
rmse_sample2 = np.sqrt(mse_sample2)
rmse_sample3 = np.sqrt(mse_sample3)
rmse_sample4 = np.sqrt(mse_sample4)print("Root Mean Squared error for Sample-1 Data is ", rmse_sample1)
print("Root Mean Squared error for Sample-2 Data is ", rmse_sample2)
print("Root Mean Squared error for Sample-3 Data is ", rmse_sample3)
print("Root Mean Squared error for Sample-4 Data is ", rmse_sample4)Mean Absolute Percentage Error (MAPE)
Mean absolute percentage error measures the accuracy as a percentage. Mathematically, it is equal to the arithmetical mean of the difference between actual and predicted value divided by actual value.
Formula for Mean Absolute Percentage Error
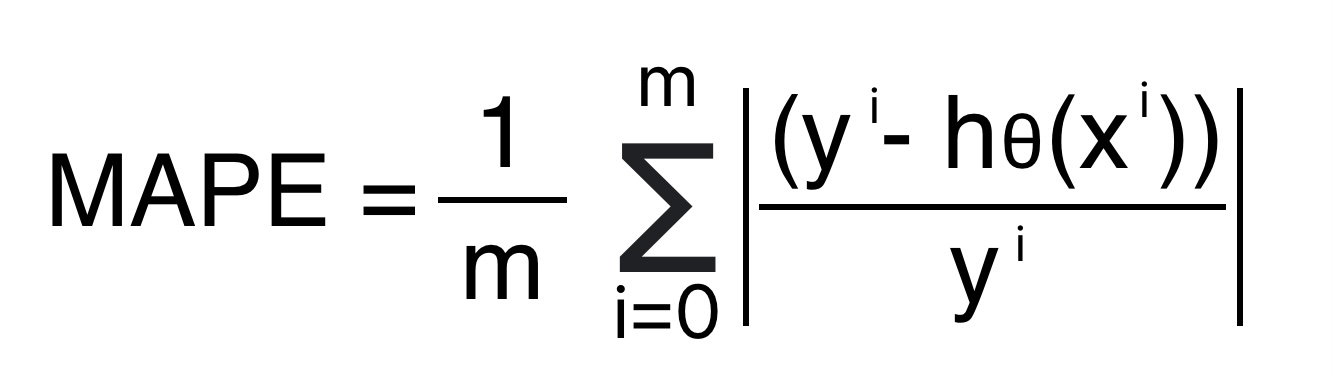
- We cannot use MAPE if the actual value is zero or close to zero because a zero in the denominator will make the error infinite.
- Penalize forecasts that are accurate for large values and reward forecasts that are inaccurate for small values.
- Easy to understand and get intrusion because output is in percentage.
Mean Absolute Percentage Error Calculation Example
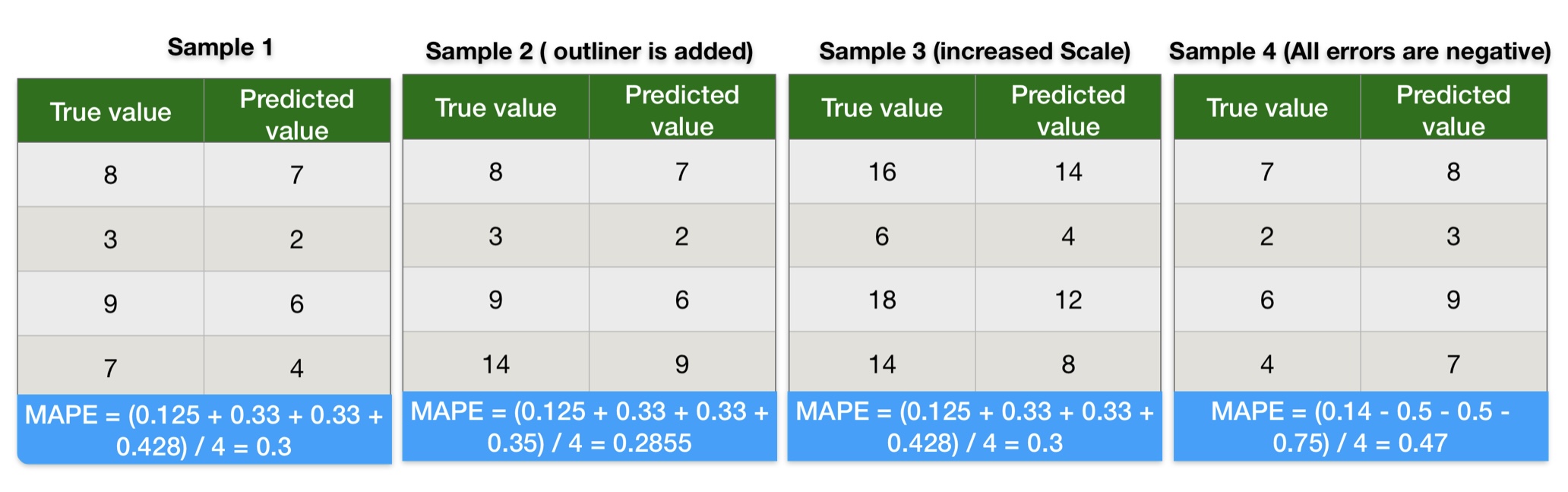
We can conclude the following points from the mean absolute percentage error calculation results:
- Results of MAPE in sample-1 and sample-2 indicate mean absolute percentage error is impacted by the outliners. Its value will be skewed with outliers.
- MAPE values in sample-1 and sample-3 indicate squaring error increases the impact of huge errors. As a result, the ML Model penalizes more if the error is large.
- Results of MAPE in sample-1 and sample-4 indicate a negative error impacts mean absolute percentage error heavily.
Python Code to Calculate Mean Absolute Percentage Error
# Import required library to measure Mean absolute percentage error
from sklearn.metrics import mean_absolute_percentage_error# Calculate Mean Absolute Percentage Error
mape_sample1 = mean_absolute_percentage_error(sample1_df["true_value"], sample1_df["predicted_value"])
mape_sample2 = mean_absolute_percentage_error(sample2_df["true_value"], sample2_df["predicted_value"])
mape_sample3 = mean_absolute_percentage_error(sample3_df["true_value"], sample3_df["predicted_value"])
mape_sample4 = mean_absolute_percentage_error(sample4_df["true_value"], sample4_df["predicted_value"]) print("Mean Absolute Percentage error for Sample-1 Data is ", mape_sample1)
print("Mean Absolute Percentage error for Sample-2 Data is ", mape_sample2)
print("Mean Absolute Percentage error for Sample-3 Data is ", mape_sample3)
print("Mean Absolute Percentage error for Sample-4 Data is ", mape_sample4)