One sample t-test is a type of t-test that is used in machine learning for hypothesis testing. This article covers one sample t-test with examples and how we can implement this in Python.

Table of Contents

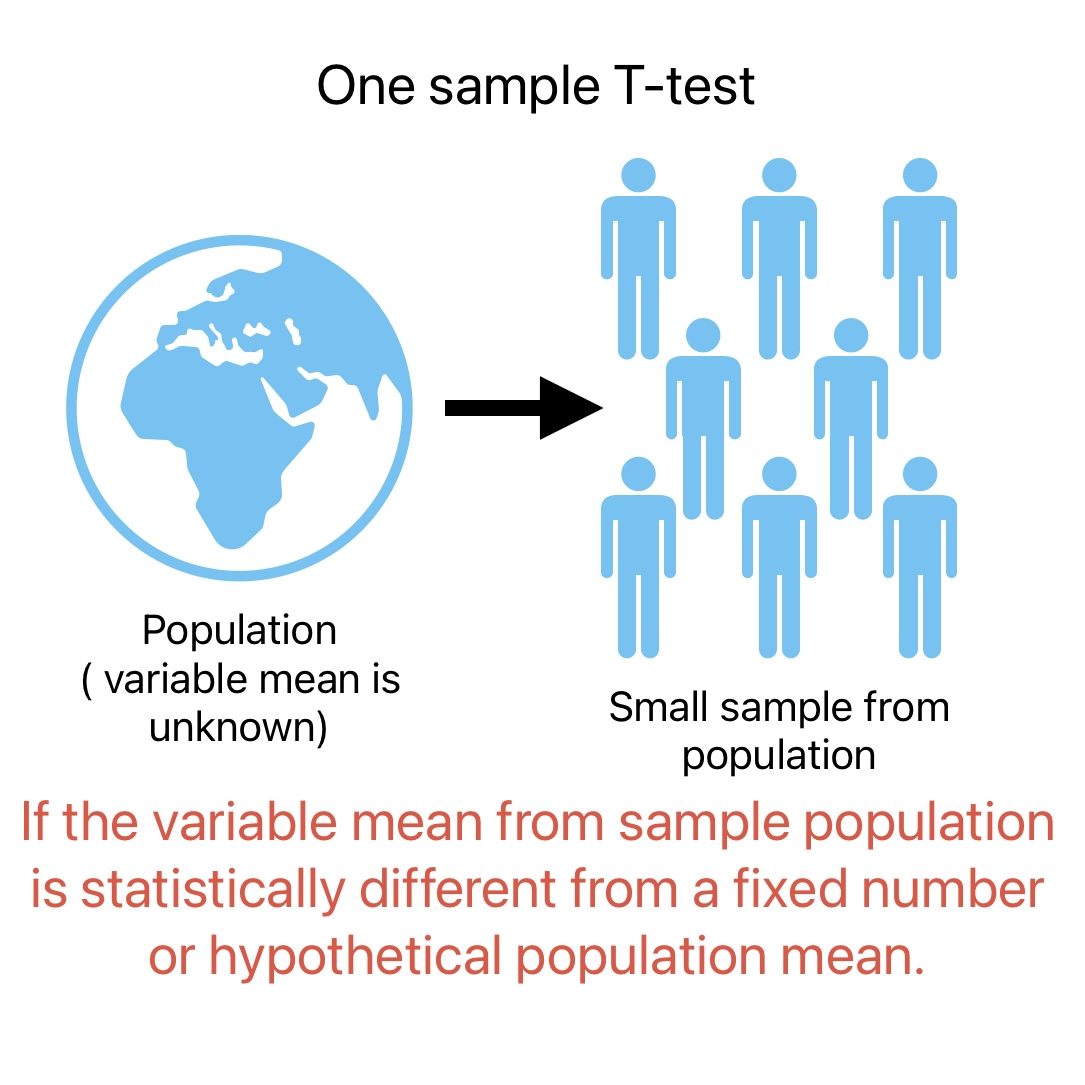
What is one Sample t-test?

One Sample t-test is a statistical t-test to determine whether a variable mean from a sample population is statistically different from a fixed number or hypothetical population mean.

Application Examples

Determine if the mean weight of the sample population is statistically different from a fixed value.
A plastic part manufacturer can use a t-test to determine if the mean product weight is 15 grams.

Prior Conditions for one Sample t-test

Following are the prior conditions for one sample t-test. We need to verify data for these points to implement one-sample t-test.

The population standard deviation is not known.
Sample Size is small (Approx. 30 samples)
Data Instances are independent.
Continuous data.
The population is normally distributed.
Sample is picked randomly from the population.

Calculation Formula for One Sample T-Test

T-test uses t distribution instead of normal distributions. The t-distribution curve has a degree of freedom equal to n-1.

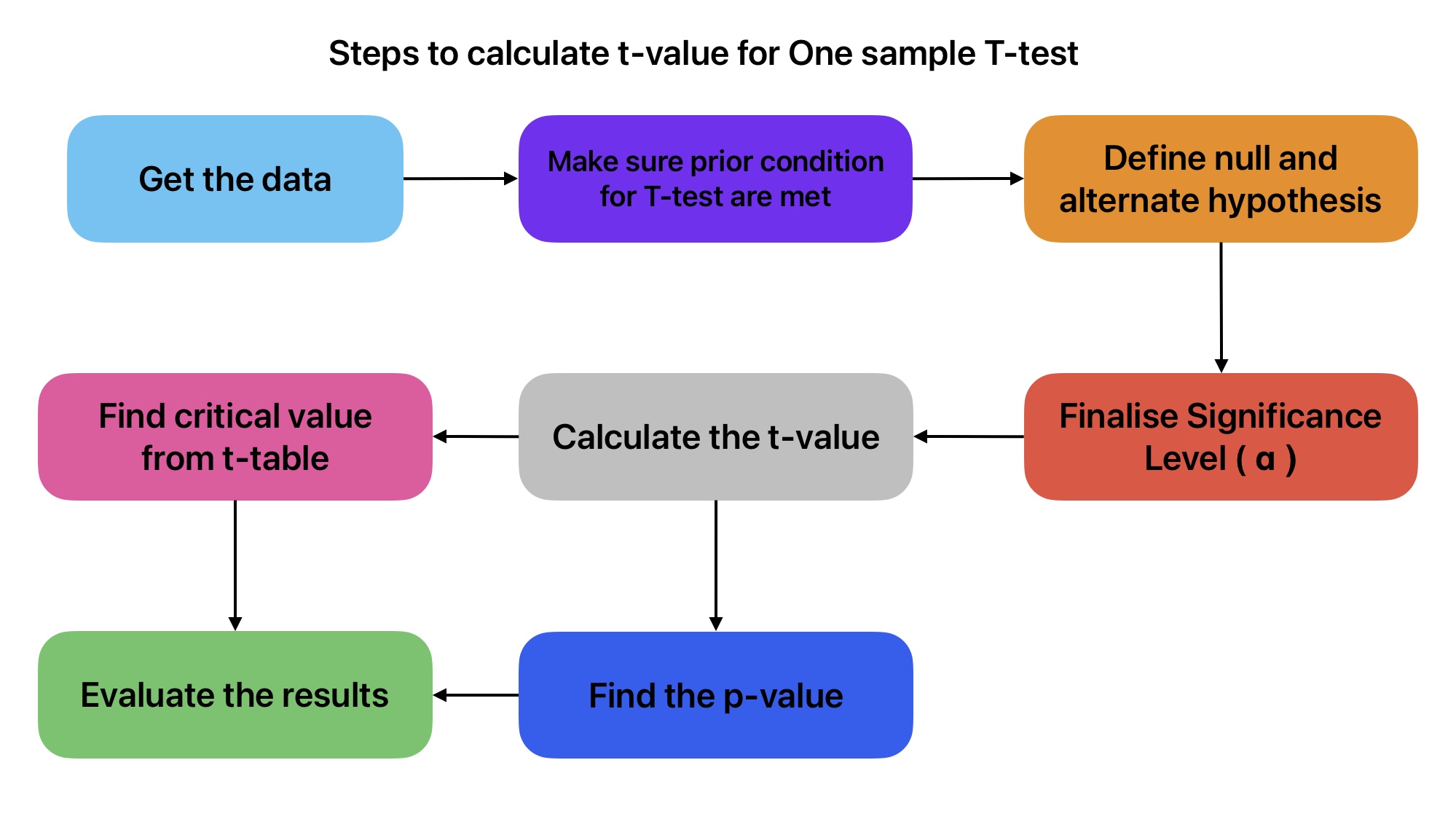
Application example for one sample t-test

Here is the list of steps to calculate the t-value and evaluate results for significance testing.

While John was working with a plastic part manufacturer, his manager came to you with the following problem.

Manager: John, is there any way to make sure the mean part weight for XYZ is 15 grams without measuring every part?

John: Yes, we can do a hypothesis test to ensure XYZ part weight is 15 grams with a 95% confidence level.

Manage: Please proceed with this and let me know the results ASAP.

John: I will collect data from production and will show you the results.

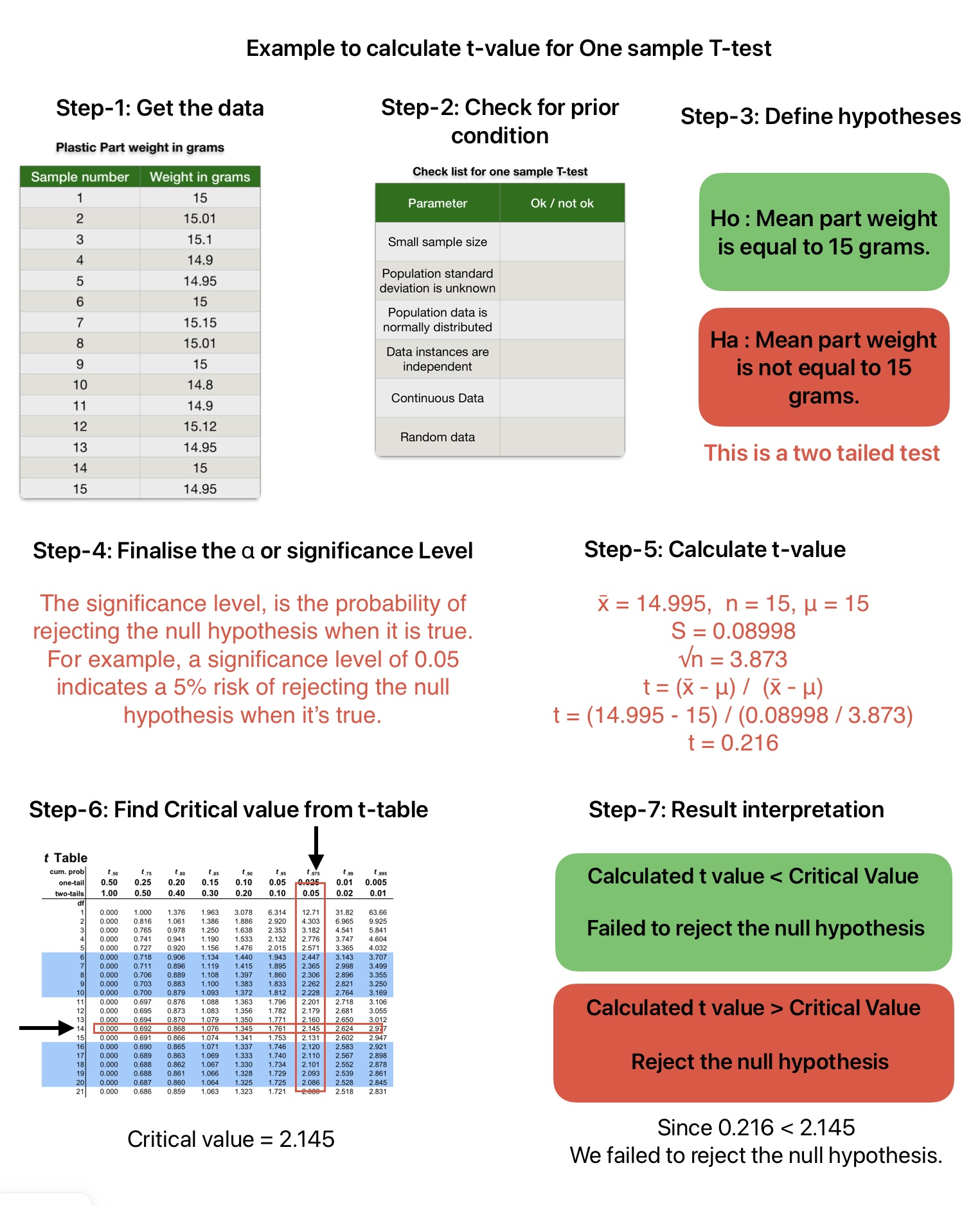
Problem Statement: We want to ensure that the manufactured part’s mean weight is 15 grams with a 95% confidence level.

Python code to implement One-sample t-test

We will implement the one-sample t-test on sample data using manual calculations and the Python SciPy Library.

Prepare for input data according to problem Statement

# Import important Library
import pandas as pd
import numpy as np

# Get the sample Weight data
sample_weight = [15, 15.01, 15.1, 14.9, 14.95, 15, 15.15, 15.01, 15, 14.8, 14.9, 15.12, 14.95, 15, 14.95]

Define Null and Alternate Hypothesis

Null Hypothesis: The mean weight of the part is equal to 15 grams.
Alternative Hypothesis: The mean weight of the part is not equal to the 15 grams.

# Define Hypothesized population mean
population_mean = 15

# Define the Significance level (alpha)
alpha = 0.05

# Calculate the Degrees of freedom
dof = len(sample_weight) - 1

Python code to calculate the t-value for One Sample t-test

# Import the Required Library
import statistics
import math

# Calculate the sample mean
sample_mean = statistics.mean(sample_weight) 
print("Sample Mean:", sample_mean)

# Calculate the sample standard deviation
sample_std = statistics.stdev(sample_weight)
print("Sample Standard Deviation", sample_std)

Sample Mean: 14.989333333333333 Sample Standard Deviation 0.08979871671582781

# Calculate t-value statistic using one sample t-test formula
calculated_t_value =  (sample_mean - population_mean) / (sample_std / math.sqrt(population_mean))
print("Calculated t-value:", calculated_t_value)

Calculated t-value: -0.4600491395693469

# Calculate Critical t-value: We can use t-table as well.
critical_t_value = stats.t.ppf(1 - alpha / 2, df=dof) 
print("Critical T-Value:", critical_t_value)

Critical T-Value: 2.1447866879169273

# Results Interpretation
if abs(calculated_t_value) > critical_t_value:
    print("Reject the null hypothesis.")
else:
    print("Fail to reject the null hypothesis.")

Fail to reject the null hypothesis.

Python code using SciPy Library to calculate the t-value

# Import SciPy Library
from scipy import stats

# Calculate t-value and p-value for One sample t test
t_value, p_value = stats.ttest_1samp(sample_weight, population_mean)

# Print the results
print("T-Value:", t_value)
print("P-Value:", p_value)

T-Value: -0.4600491395693468 P-Value: 0.6525446094245332

# Result Interpretation by comparing p_value and significance level
if abs(p_value) < alpha:
    print("Reject the null hypothesis.")
else:
    print("Fail to reject the null hypothesis.")

Fail to reject the null hypothesis.

Now you go to your boss to show him the results.

Manage: John, have you got the results?

John: Yes, the results are in our favor. We failed to reject the null hypothesis. With a 95% confidence level, we can say the part weight is 15 grams.

Manager: Good, what variation we can expect in this part weight?

John: For this, we need a Confidence Interval. (You can read more about Confidence Interval Here)

Manager: Please present these results as well.

One Sample T-test for Significance Testing