NumPy stands for Numerical Python. NumPy Library is an open-source library in python to perform day to day machine learning tasks. We use NumPy functions for matrix, mathematical and functional calculations. This article covers functions in NumPy Library for machine learning.
We suggest you also read this article on Pandas Library for Machine Learning.
Table of Contents
ToggleKey Features of NumPy Library
Here is the list of key NumPy library for machine learning features:
- High Performance.
- Broadcasting Functions.
- Integrate code from C and C++.
- Works with various databases.
Getting Started with NumPy Library for Machine Learning
The first step to start with numpy library for python is to install it and load in your program.
How to Install NumPy Library?
conda install numpy
pip install numpyHow to import NumPy library in your code?
import numpy as npHow to import and export data in your code using NumPy Library?
# Load data from csv file
np.genfromtxt (filename.csv, delimiter=",")
# Write data to text file
np.savetxt ( "saved_file.txt", array_name, delimiter="")
# Write data to csv file
np.savetxt("saved_file.txt", array_name, delimiter=",")
Uses of NumPy in Machine Learning
Here is the list of the uses of NumPy library in machine learning.
- Create, copy, and view array
- Generate Numbers and multi dimension array
- Statistical Calculations
- Matrix Calculations
- Vector Math Operations
- Scalar math Calculations
- Search, sort, and Count Data : Bitwise Operators
- Modification of array: Combine, split, Stacking
- Broadcasting
1. Create, copy and view Array in NumPy Library
An array in numpy also known as NumPy array consist of a collection of values or variables. Each of these values are assigned an indices. An array in numpy library can have one or multiple dimensions.
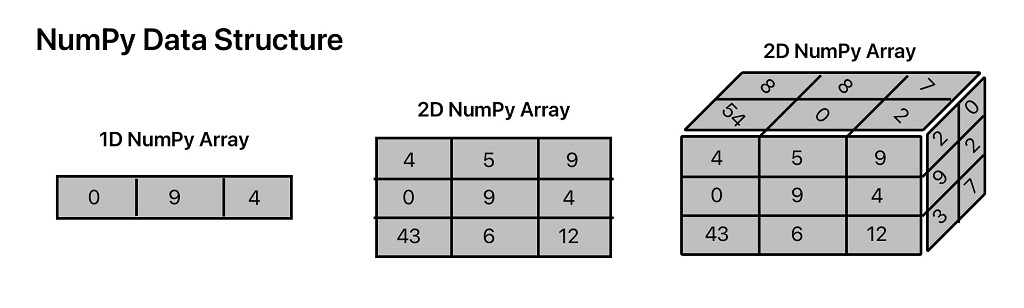
Python code to create a Scalar number, 1D, 2D & 3D array
# Create a scalar number
x = np.array (6)
print(x)6
# Create a 1D array or vector
x = np.array ([1,2,3,4])
print(x)[1 2 3 4]
# Create a 2D array or vector
x = np.array ([[1,2],[3,4]])
print(x)[[1 2] [3 4]]
# Create a 3D array or vector
x = np.array ([[[1,2],[3,4]],[[5,6],[7,8]]])
print(x)[[[1 2] [3 4]] [[5 6] [7 8]]]
2. Generate numbers and Multi-dimension array
#Create a 2X2 zero Matrix
np.zeros((2, 2))array([[0., 0.],
[0., 0.]]) #Create a 2X2 array with all values equal to 1
np.ones((2, 2))array([[1., 1.],
[1., 1.]]) #Create a 2X2 identity matrix
np.eye(2, 2)array([[1., 0.],
[0., 1.]]) #Create a random array
np.random.random(2)array([0.61665673, 0.17356949])
#Create an array of 6 evenly divided values from 0 to 100
np.linspace(0, 100, 6)array([ 0., 20., 40., 60., 80., 100.])
#Create an array of values from 6 to 20 with a step of 3
np.arange(0, 20, 3)array([ 0, 3, 6, 9, 12, 15, 18])
#Create an array of all values equal to 5
np.full((2,2),5)array([[5, 5],
[5, 5]]) #Create an 4X5 matrix of random floats between 0 to 1.
np.random.rand(4,5)array([[0.63007838, 0.96420293, 0.12285109, 0.57142873, 0.32202221],
[0.8590761 , 0.95756662, 0.94256112, 0.42173919, 0.3076715 ],
[0.36684542, 0.35649315, 0.34992426, 0.87794128, 0.7660394 ],
[0.83144068, 0.24431553, 0.97929444, 0.97706818, 0.0228844 ]]) #Create an 4X5 matrix of random floats between 0 to 100.
np.random.rand(4,5)*100array([[62.2863148 , 61.70591268, 80.5048827 , 91.42682108, 95.27486056],
[25.87264292, 23.09018856, 62.13470533, 82.74979684, 52.48818638],
[88.92828787, 34.37572344, 13.40762842, 38.37105785, 53.48873601],
[36.33198314, 86.58847449, 78.99792287, 42.30833456, 26.81819272]]) #Create an 2x3 matrix with random integers between 0 to 4.
np.random.randint(5, size=(2,3))array([[1, 4, 2],
[0, 3, 1]]) 3. Statistical Calculations using NumPy Library in Python
Calculate the Mean
# Calculates the mean along the rows
x=np.random.rand(4,5)
x_mean_r=np.mean(x, axis=0)
print(x)
print("mean along the columns in array x=", x_mean_r)[[0.43393595 0.12069357 0.76235215 0.39258262 0.87983847] [0.11492885 0.82122427 0.86832896 0.15272799 0.80778245] [0.24944495 0.51173666 0.90899038 0.06282514 0.45795923] [0.22181823 0.29105218 0.60932245 0.87320688 0.67979183]] mean along the columns in array x= [0.25503199 0.43617667 0.78724848 0.37033566 0.706343 ]
# Calculates the mean along the columns
x=np.random.rand(4,5)
x_mean_c=np.mean(x, axis=1)
print("mean along the columns in array x=", x_mean_c)mean along the columns in array x= [0.560136 0.32332387 0.36520071 0.56531737]
Calculate minimum and maximum values in an array
# output the minimum value in an array
x=np.random.rand(4,5)
x_min=np.min(x)
print("minimum value in array x=", x_min)
minimum value in array x= 0.19072417836680666
# output the maximum value in an array
x=np.random.rand(4,5)
x_max=np.max(x)
print(x)
print("maximum value in array x=", x_max)
[[0.44291462 0.18402595 0.76225259 0.22432479 0.72919081]
[0.29469839 0.41962133 0.96848737 0.58147487 0.48804411]
[0.95388017 0.84010951 0.40962723 0.32830566 0.50249811]
[0.16367611 0.22980977 0.62859858 0.29352372 0.46691278]]
maximum value in array x= 0.9684873715615953
# output the minimum values across rows in an array
x=np.random.rand(2,2)
x_min_r=np.max(x, axis=0)
print(x)
print("minimum value in array x across rows=", x_min_r)
# Similarly we can calculate maximum values across rows or columns.
[[0.92572232 0.18691117] [0.19464648 0.29460877]] minimum value in array x across rows= [0.92572232 0.29460877]
Calculate Variance using NumPy Library
# output the variance across the specified axis
x=np.random.rand(2,2)
x_var_r=np.var(x, axis=0)
print(x)
print("Variance of x across rows=", x_var_r)
# Similarly we can calculate variance across columns or total variance in array.
[[0.05839632 0.72993163] [0.4491669 0.14340383]] Variance of x across rows= [0.03817541 0.08600371]
Standard Deviation
# output the Standard Deviation the specified axis
x=np.random.rand(2,2)
x_std_r=np.std(x, axis=0)
print(x)
print("Standard Deviation of x across rows=", x_std_r)
# Similarly we can calculate standard deviation using numpy library across columns or total standard deviation in array.
[[0.35272972 0.73295582] [0.39086507 0.83280346]] Standard Deviation of x across rows= [0.01906767 0.04992382]
Correlation Coefficient
corrcoef() function in numpy library is used to compute the Pearson correlation coefficient between two or more arrays. The Pearson correlation coefficient is a measure of the linear relationship between two variables, and it ranges from -1 to 1. A value of 1 indicates a perfect positive correlation, -1 indicates a perfect negative correlation, and 0 indicates no correlation.
x = np.array([1, 2, 3, 4, 5])
y = np.array([2, 3, 4, 5, 6])
# Calculate the Pearson correlation coefficient
correlation_coefficient = np.corrcoef(x, y)[0, 1]
print(f"Pearson correlation coefficient: {correlation_coefficient}")Pearson correlation coefficient: 0.9999999999999999
4. Matrix operations in NumPy Library
Matrix dot product in NumPy
Dot product for two matrix is equivalent to the product of two matries. Prior conditions for dot product is the number of columns in first matrix shall be equal to the number of rows in second matrix.
For example, if a matrix A and B shape is (3X2) and (2X3) respectively. The shape of matrix after dot product of A and B will be 3X3.
# Dot product for two metrices A and B
#Create a 2X2 Matrix A
A = np.array([[1, 2], [3, 4]], dtype=np.float64)
#Create a 2X3 Matrix B
B = np.array([[1, 2, 3], [4, 5, 6]], dtype=np.float64)
#Create a new matrix C with a dot product of matrix A and B
C = A.dot(B)
print("The matrix c is:", C)
print("The shape of new matrix c is:", C.shape)
The matrix c is: [[ 9. 12. 15.] [19. 26. 33.]]
The shape of new matrix c is: (2, 3)
Transpose of a matrix in NumPy
We can use Numpy library function to transpose a matrix to convert rows into columns and columns in rows.
# Transpose of a matrix
#Create a 2X3 Matrix B
B = np.array([[1, 2, 3], [4, 5, 6]], dtype=np.float64)
print("the shape of matrix B is:", B.shape)
# Now we will create a new matrix Y that will be a transpose of B
Y=np.transpose(B, (1,0))
print("the shape of new matrix Y is", Y.shape)the shape of matrix B is: (2, 3)
the shape of new matrix Y is (3, 2)
Reshape data in NumPy
We can use NumPy library to reshape a matrix to change a matrix dimensions while ensuring number of elements in matrix are same.
# Reshape data in numpy
X = np.array([1, 2, 3, 4, 5, 6])
print("shape of the input array is", np.shape(X))
Y=np.reshape(X, (2,3))
print("shape of the input array is", np.shape(Y))shape of the input array is (6,)
shape of the input array is (2, 3)
If we use -1 as number of columns, it will automatically calculates the number of columns.
# Reshape data using numpy Library
X = np.array([1, 2, 3, 4, 5, 6])
print("shape of the input array is", np.shape(X))
Y=np.reshape(X, (3,-1))
print("shape of the input array is", np.shape(Y))shape of the input array is (6,)
shape of the input array is (3, 2)
5. Vector Math Operations in NumPy Library
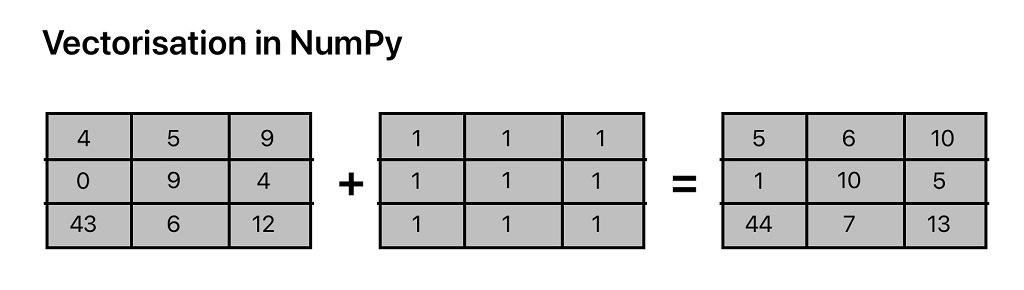
Add Values Elementwise
# Add Values element wise
x = np.array([[1, 2], [3, 4]])
y = np.array([[5, 6], [7, 8]])
z1 = np.add(x,y)
print(f"The sum of two matrix will be: \n {z1}")
# We can use x+y to calculate the sumThe sum of two matrix will be:
[[ 6 8] [10 12]]
Subtract Values Elementwise
# Subtract Values element wise
x = np.array([[1, 2], [3, 4]])
y = np.array([[5, 6], [7, 8]])
z1 = np.subtract(x, y)
print(f"The subtraction of two matrix will be: \n {z1}")
# We can use x-y to calculate the sumThe subtraction of two matrix will be:
[[ -4 -4] [-4 -4]]
How to Multiply Values Elementwise
# multiply Values element wise
x = np.array([[1, 2], [3, 4]])
y = np.array([[5, 6], [7, 8]])
z1 = x*y
print(f"The elementwise multiplication of two matrix will be: \n {z1}")
# We can use np.multiply(x, y) to multiply ValuesThe elementwise multiplication of two matrix will be:
[[ 5 12] [21 32]]
How to divide Values Elementwise in an array
# multiply Values element wise
x = np.array([[1, 2], [3, 4]])
y = np.array([[5, 6], [7, 8]])
z1 = x/y
print(f"The elementwise division of two matrix will be: \n {z1}")
# We can use np.divide(x, y) to multiply ValuesThe elementwise division of two matrix will be:
[[0.2 0.33333333]
[0.42857143 0.5 ]]
Raise to power values elementwise in an array
# Raise to power values element wise
x = np.array([[1, 2], [3, 4]])
y = np.array([[2, 1], [1, 2]])
z1 = np.power(x,y)
print(f"The elementwise of matrix x to y will be: \n {z1}")The elementwise of matrix x to y will be:
[[ 1 2] [ 3 16]]
Elementwise Boolean Operation in python using Numpy
# Elementwise Boolean Operation in python using Numpy Library
x = np.array([[1, 2], [3, 4]])
y = np.array([[0, 2], [1, 4]])
z1 = np.equal(x,y)
print(f"The resultant matrix after comparing x to y will be: \n {z1}")The resultant matrix after comparing x to y will be:
[[False True] [False True]]
Calculate Square-Root, natural log and sin of an array
#Calculate Square-root, natural log and sin of all elements in an array
#Define an array
x = np.array([[1, 2], [3, 4]])
# Calculate and print the squareroot of an array
z1 = np.sqrt(x)
print(f"The squareroot of matrix x will be: \n {z1}")
z2 = np.sin(x)
print(f"The sine of matrix x will be: \n {z2}")
z3 = np.log(x)
print(f"The log of matrix x will be: \n {z3}")The square-root of matrix x will be:
[[1. 1.41421356] [1.73205081 2. ]]
The sine of matrix x will be:
[[ 0.84147098 0.90929743] [ 0.14112001 -0.7568025 ]]
The log of matrix x will be:
[[0. 0.69314718] [1.09861229 1.38629436]]
6. Search, Sort and Count Data
We can extract any specific number from an array using Indexing function in numpy library. NumPy array index starts from 0, and -1 is last element in array.
Search a value by index position in 1D array
x = np.array([1, 2, 3, 4])
#This will print value at index 0 = 1
print("value at index 0:", x[0])
#This will print the last value in index = 4
print("value at last index:",x[-1]) value at index 0: 1
value at last index: 4
Search a value by index position in multi dimension array
x = np.array([[1, 2, 3], [4, 5, 6]])
# This will print value at index (0, 1). Value at first row and second column(2).
print("Value at first row and second column:", x[0, 1])
# This will print all elements in the second column [2 5]
print("elements in the second column:", x[:,1])
# This will print all elements in the first row [1 2 3]
print("elements in the first row:", x[0,:])
# This will print all elements in the first row starting from second column [2 3]
print("elements in the first row starting from second column:", x[0, 1:])
# This will print first and second elements in the second row [4 5]
print("first and second elements in the second row:", x[1, :2])Value at first row and second column: 2
elements in the second column: [2 5]
elements in the first row: [1 2 3]
elements in the first row starting from second column: [2 3]
first and second elements in the second row: [4 5]
Boolean Array Indexing
# Boolean array Indexing
x = np.array([[1, 2, 3], [4, 5, 6]])
# Index values as true or false in an arrray
print ("is values in an array greater than 3:", x > 3)
# Get all values in an array greater than a scalar number
print ("values in an array greater than 3:", x[x > 3])is values in an array greater than 3: [[False False False] [ True True True]]
values in an array greater than 3: [4 5 6]
Know about the NumPy Array
# Know about numpy array
x = np.array([[1, 2, 3], [4, 5, 6]])
# Determine the shape of the array x (rows, columns)
print("The shape of the array is:", x.shape)
# Determine the total element in the array x
print("The total elements in the array is:", x.size)
#Find data type of the array x
print("The shape of the array is:", x.dtype)The shape of the array is: (2, 3)
The total elements in the array is: 6
The shape of the array is: int32
7. Modification of array: Combine, split, Stacking
Concatenate two matrix
# Concatenate two matrix
x = np.array([[1, 2], [3, 4]])
print("The shape of existing matrix x is:", x.shape)
# Add a matrix as new rows
y1 = np.concatenate ([x, x], axis=0)
print("The shape of new matrix y1 (new rows are added) is:", y1.shape)
# Add a matrix as new Columns
y2 = np.concatenate ([x, x], axis=1)
print("The shape of new matrix y2(new columns are added) is:", y2.shape)The shape of existing matrix x is: (2, 2)
Shape of new matrix y1 (new rows are added) is: (4, 2)
The shape of new matrix y2(new columns are added) is: (2, 4)
Stacking
#Stacking Will make a 2 dimension matrix into 3 dimension
x = np.array([[1, 2], [3, 4]])
print("The shape of existing matrix x is:", x.shape)
# Stack a matrix on one another
y1 = np.stack([x, x], axis=0)
print("The shape of new matrix y1 (new rows and columns are added in new dimension) is:", y1.shape)The shape of existing matrix x is: (2, 2)
The shape of new matrix y1 (new rows and columns are added in new dimension) is: (2, 2, 2)
Change NumPy array using Indexing
#Change numpy array using Indexing
x= np.array([1, 2, 3, 4])
#This will replace the value of index 1 in array x with 5. New array will be. [1, 5, 3, 4]
x [1] = 5
print("The new array x is:", x)The new array x is: [1 5 3 4]
Convert a numpy array to a Python list
#Convert a numpy array into python list
x= np.array([1, 2, 3, 4])
print("The instance x is a numpy array:",isinstance(x, np.ndarray))
y=x.tolist()
print("New instance y is a numpy array:",isinstance(y, np.ndarray))
print("The new instance y is a Python list:",isinstance(y, list))The instance x is a numpy array: True
New instance y is a numpy array: False
The new instance y is a Python list: True
How Numpy array are different from Python Lists and Pandas Data Frame
Numpy array is an alternative to python lists and has the following advantages.
- Holds less memory
- Faster processing
- Numpy array needs to be homogenous. In other words, it cannot have numerical and string data types.
| Parameter | Python List | NumPy Array | Pandas Data Frame |
|---|---|---|---|
| Storage | Dynamic | Fixed | - |
| Speed | Slow due to type checking | Fast due to vector operations | Slower than NumPy array |
| Data Type | Hetrogeneous: Can have different data type. | Homogeneous: Can not have different data types, | Hetrogeneous: Can have different data type. |
| Data Access | - | Index Positions | Index Positions or index labels |
| Complex Math operations | NA | Possible | Possible |
| Broadcasting and Vectorization | NA | Possible | Possible |
| Memory | Less | More than Python List | More than NumPy Array |
| Number of Dimensions | By defalt: 1D. Multi-dimension data adds complexity | Multi-dimension array | 2D Array |
