Regularization in machine learning is a technique to prevent the overfitting problem in machine learning models. Overfitting is a problem in ML models where the ML model performs well on training data but does not generalize on unseen data.
Table of Contents
ToggleWhat is Regularization in Machine Learning?
Regularization in machine learning is a technique for constraining or regularizing machine learning models by constraining the weights or parameters to solve the over-fitting problem.
We need to scale the data before applying a regularized machine-learning algorithms.
How does Regularization in Machine Learning Work?
Regularization in machine learning adds a penalty term to the machine learning model cost function. This penalty term discourages the ML model from overfitting the training, resulting in a simpler and more robust machine learning model.
Cost Function with Regularization = Cost Function + α * Regularization Term
- α is a hyperparameter that controls the regularization strength.
- The larger the value of α, the stronger will be the regularization.
- α controls the trade-off between fitting training data and ML model simplicity.
The goal of the Machine Learning model with regularization is to determine the weights that minimize the cost function.
Regularization Techniques in Machine Learning
Here is the list of techniques we can use to regularize the machine learning models.
- Ridge Regression
- Lasso Regression
- Elastic Net
Ridge Regression (L2 Regularization)
Ridge regression is also known as L2 Regularization or Tinkhonov Regularization. In this, a regularized term is added to the linear model cost function during training. This additional regularized term solves the problem of multicollinearity and overfitting of training data.
Cost Function for L2 Regularization

During Ridge regularization in machine learning we tries to find the values for θ that minimizes the cost function for ridge regression. We can conclude on following points from the formula for L2 Regularization.
- The biased error (θ0) is not included in the regularization term. Therefore j value starts from 1 not 0.
- The regularized term is used during training, not during validation. Therefore the cost function used during training will be different from validation.
- L2 regularization ensures the model parameters are as small as possible.
- Hyperparameter (alpha) controls the extent or strength of regularization of the linear model.
- The regularization term encourages the model to keep the weights as small as possible to prevent overfitting.
Can we use ridge regression for classification ML algorithms?
As the name suggests, Ridge Regression was originally used to solve regression problems where we predict a continuous output. We can not use it for classification problems because it does not give a class probability.
However, we can use the L2 regularization in machine learning for classification in logistic regression using the sci-kit-learn library.
How Regularization Hyperparameter (α) impacts the cost function
Ridge regression hyperparameter “α” is a positive constant that controls regularisation strength. Its value can be any positive number and depends on the specific problem. The common alpha values are 0.001, 0.01, 0.1, 1, 10, 100.
The best practice during machine learning model development is to select different alpha. Afterward, observe their impact on model performance using cross-validation. Here is the list of factors that afftes the Ridge regression hyperparameter alpha:
- Characteristics of data.
- Multi-colinearity in data
- Bias-variance trade-off
Python code for Ridge Regression Implementation
We can use the following two techniques or methodologies to implement the Ridge Regression in Python.
1. Solve a Closed Form Equation
2. Using Gradient Decent
The selection of the technique depends on the number of features and data points. In Python, we can use the sci-kit-learn library to implement Ridge Regression.
# Import Required Library
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler# Create a random dataset
np.random.seed(42)
m = 50 # Number of samples
X= 3 * np.random.rand(m , 1) # np.random.rand(m,1) will generate m random numbers from 0 to 1
y = 2 + 1.5 * X + np.random.randn(m,1)/1.5
#Plot input training data
plt.plot(X, y, "b.")
plt.xlabel("$X$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.show()Python code for Ridge Regression using Closed Form Equation
# Train the ridge linear regression machine learning Model
from sklearn.linear_model import Ridge
ridge_reg = Ridge(alpha=1, solver="cholesky", random_state=42) #we can also use solver="sag" as well
ridge_reg.fit(X, y)# Predict values
ridge_reg.predict([[5]])array([[9.17569464]])
Python code for Ridge Regression using Gradient Descent
# Import Required Library
from sklearn.linear_model import SGDRegressorsgd_reg = SGDRegressor(penalty="l2",max_iter=1000, tol=0.001, random_state=42)
sgd_reg.fit(X, y.ravel())
# array.ravel() functions returns contiguous flattened array(1D array with all the input-array elements).# Predicting Unknown Values
sgd_reg.predict([[5]])array([10.07089592])
Lasso Regression (L1 Regularization) in machine learning
Lasso regression is also known as L1 Regularization or “Least Absolute Shrinkage and Selection Operator Regularization”. In this, a regularized term is added to the model cost function during training.
Cost Function for Lasso Regression

- Lasso regression may eliminate the weights of the least important features. Therefore it also works as a feature selection algorithm.
- Lasso produces sparse models, where many coefficients are zero. These models are easy to interpret and may generalize well when working with high-dimensional data.
- The L1 Regularization machine learning model effectively handles the multicollinearity because it will select one feature and make the other feature weight zero.
How Regularization Hyperparameter (α) impacts the L1 Regularization Best Fit Line
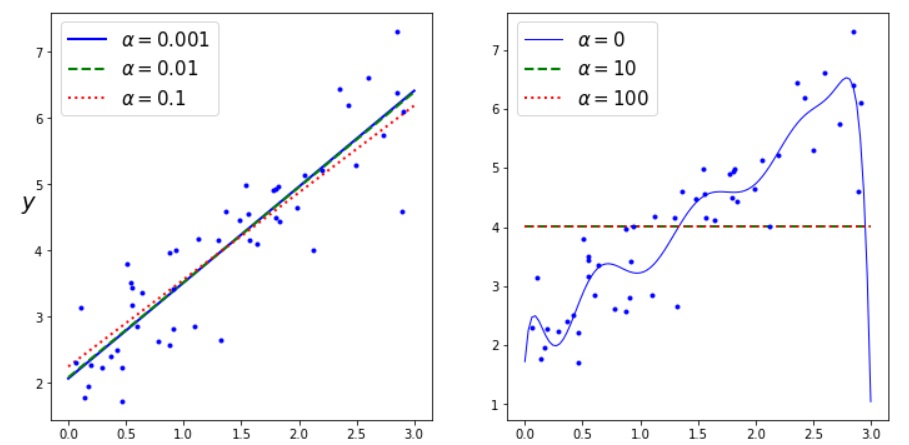
The regularization hyperparameter (α) in Lasso Regression influences the best-fit line by controlling the amount of regularization in machine learning.
- As the value of alpha increases, the regularization term becomes more prominent and the coefficient for a few features tends to become zero.
- A smaller value of alpha makes the model more complex.
- Smaller alpha results in low bias and high variance. As a result, training data may overfit the ML model.
- Larger alpha results in high bias and low variance.
- The optimal value for α depends on the specific dataset and the trade-off between fitting the training data well and preventing overfitting.
Python code for Lasso Regression Implementation
# Create a random dataset
np.random.seed(42)
m = 50 # Number of samples
X= 3 * np.random.rand(m , 1)
y = 2 + 1.5 * X + np.random.randn(m,1)/1.5#Import the required Library
from sklearn.linear_model import Lasso
# Define the Model
lasso_reg = Lasso(alpha=0.1)
#Fit the model
lasso_reg.fit(X, y)lasso_reg.predict([[5]])array([8.81865465])
Elastic Net
Elastic Net comes in between Ridge and Lasso Regression. It includes both Ridge and Lasso’s regularization terms along with mix ratio r.
When
- r = 0, Elastic Net is equivalent to Ridge Regression.
- r = 1, It is equivalent to Lasso Regression.
Cost Function for Elastic Net Regression
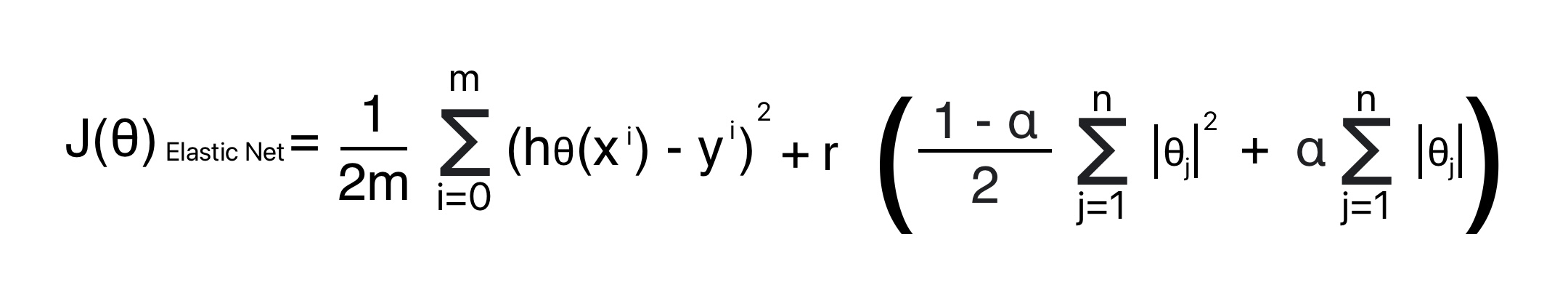
Python code for Lasso Regression Implementation
# Import required Library
from sklearn.linear_model import ElasticNet
# l1_ratio corresponds to the mix ratio r
elastic_net = ElasticNet(alpha=0.1, l1_ratio=0.5)
#Fit the ML model
elastic_net.fit(X, y)# Predict Un known Values
elastic_net.predict([[5]])array([8.74539482])
Elastic Net regularization in machine learning is preferred over Lasso because of the following reasons:
- Lasso regression may behave erratically when the number of features is greater than the number of training instances.
- When several features are strongly correlated.
