Linear Regression makes few assumptions about the training data, to deliver a solution. We will not get good results if the data does not fulfill these assumptions. Therefore, the best practice is to verify the data on assumptions of linear regression before proceeding with linear regression analysis in data science.
Table of Contents
ToggleWhat are the Assumptions of Linear Regression
Here is the list of prior conditions or assumptions of linear regression machine learning model. We need to ensure these assumptions are fulfilled before implementing linear regression.
- Linear Relationship between independent and dependent variable
- Multi-collinearity does not exist in data
- No Auto-correlation exists
- Homoscedasticity
- Normally Distributed Prediction Error
Linear Relationship between independent and dependent variable
The first assumptions for linear regression is linear relationship between the independent and dependent variables. In other words, the change in “y” due to change in “X” is constant.
A linear line will not generalize on training and un-seen data if the relationship between the dependent and independent variables is non-linear.
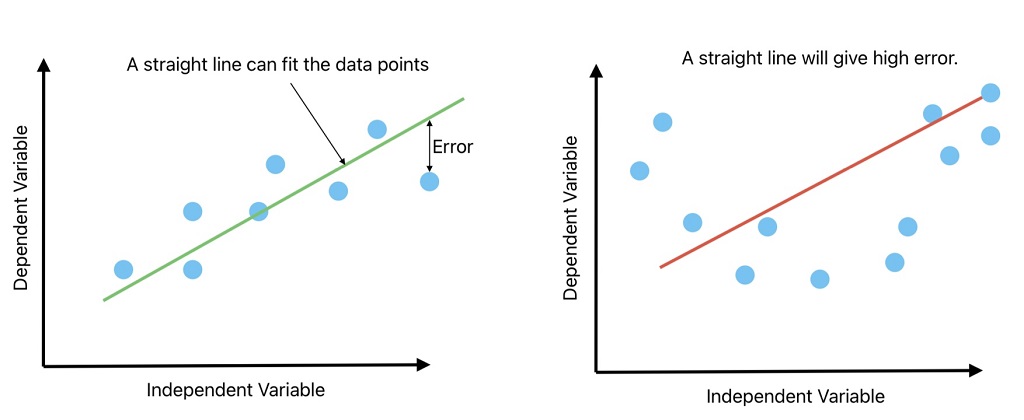
- In the left image, a linear line fits on training data with high accuracy.
- Whereas, when the data is non-linear, the accuracy decreases drastically with a linear line.
Multi-collinearity does not exist in data
Multi-collinearly is a condition where two or more features or independent variables are highly correlated with one another.
For example, if you are predicting the distance traveled by a body using its acceleration and velocity with time. These two variables are highly correlated. Here, we don’t need two variables to predict the traveled distance. Only one variable can solve the problem.
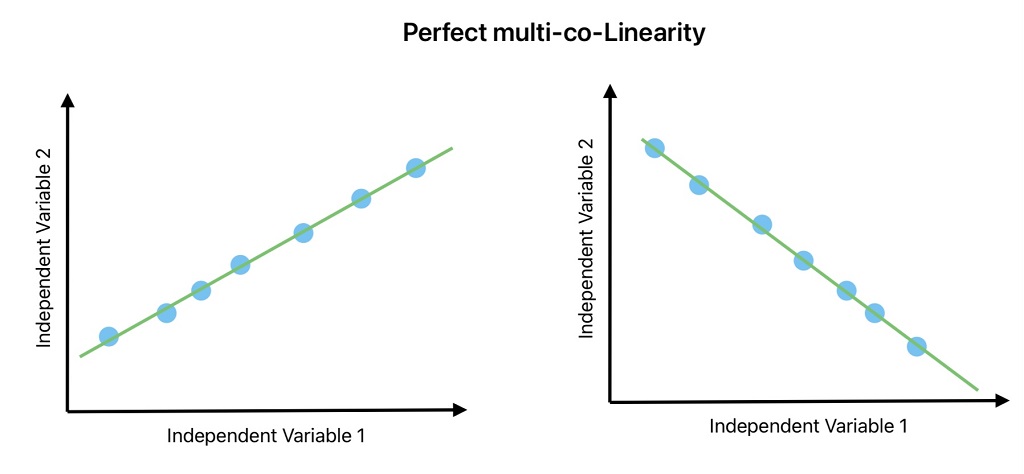
The prior assumptions of linear regression is the multi-colinearity does not exists in data.
How multi-collinearly impacts the outcome of Linear Regression?
Two collinear variables contain the same information. Therefore if our data have highly correlated variables.
- We don’t know which variable is predicting the outcome.
- It becomes difficult to estimate the parameters correctly because a change in one variable will change another.
- ML model complexity increases without any value addition.
How to check for multi-co-linearity in data
We can use one of the following techniques to determine multi-co-linearity in data:
- Scatter Plots
- Correlation Table
- VIF Factor. If VIF <= 4 => Less Correlation, If MIF ≥= 10 => High Correlation
How to solve multi-colinearity issues from data?
We can solve multi-co-linearity problems in data for linear regression using following techniques:
- Remove or combine highly correlated features in data.
- Use only relevant features
- Lasso and Ridge regression
No Auto-correlation exists: Prior Assumptions of Linear Regression
Auto Correlation represents the degree of similarity between a given time series (at time t) and lagged time (at time t-1). It exists within a variable and has no relationship with other variables.
For example, if today’s weather is sunny, it is more likely tomorrow will also be sunny. Here tomorrow is more likely to be sunny because of today.
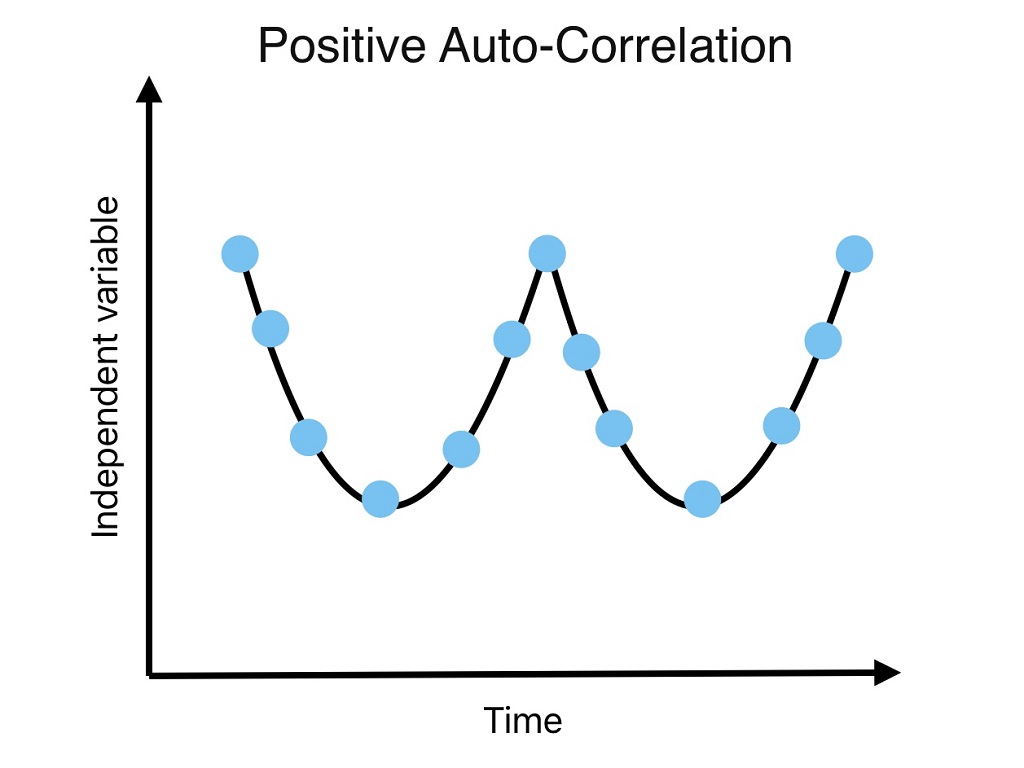
We cannot apply linear regression if this kind of relation exists because data is independent is a prior condition for linear regression analysis. Whereas, auto-correlation suggests data is correlated or is not independent. Therefore, we need to check these assumptions of linear regression.
How auto-correlation impacts Linear Regression Performance
Auto-correlation significantly impacts Linear Regression Performance in the following ways.
- Correlated errors resulting from auto-correlation can inflate or deflate the estimated parameters.
- Correlated data will not add any value to the performance of the ML algorithm.
- A small change in the data may lead to significant variations in the estimated parameters. And this is reflected in predicted values. Therefore Linear regression models with auto-correlation are less stable.
- It becomes difficult to determine patterns in data.
How to check for auto-correlation in data
We can check the correlation in data using the following parameter.
- A plot between residuals over time to determine the pattern in data.
- Durbin-Watson Statistic: Its values vary from 0 to 4. DW= 2 implies No Autocorrelation, 0 = DW ≤ 2 implies Positive Autocorrelation, 2 ≤ DW < 4 implies a Negative Autocorrelation
How to solve auto-correlation in data
It is important to correct auto-correlation in data to ensure the quality of linear regression predictions. We can use one of the following techniques to handle autocorrelation.
- Use of lagged variables as an input to time series data. For example, if you are predicting a stock price. We know that to some extent today’s stock price is dependent on yesterday’s price. Therefore data is autocorrelated. We can solve this problem by including yesterday’s price as an input to today’s price.
- We can use the difference in value instead of the actual value as an input to remove the impact of autocorrelation.
- Use of autoregressive integrated moving average (ARIMA) and autoregressive conditional heteroskedasticity (ARCH) models. These models are designed to deal with autocorrelation and time-series data.
Homoscedasticity: Assumptions for Linear Regression
Homoscedasticity ensures constant variance in error in the data across all levels of independent variables.
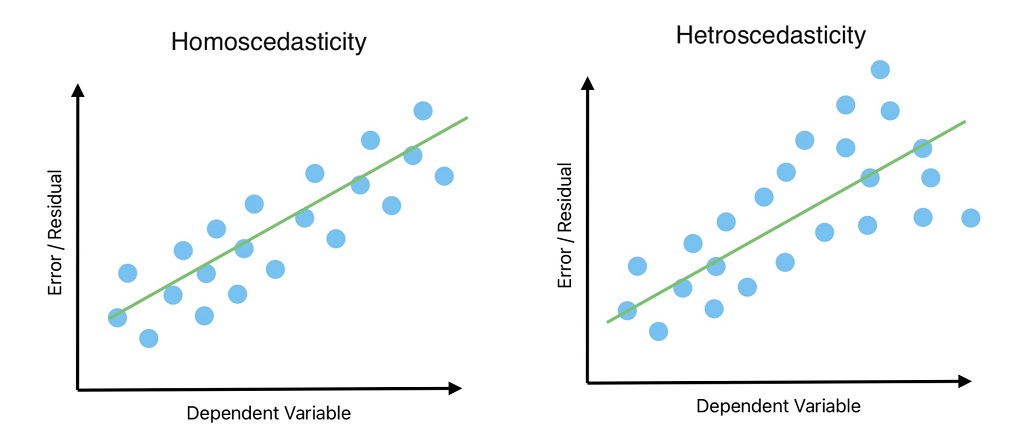
Any outliner in data can result in non-constant variance because the outliner results in high weight and impacts the model performance.
The opposite of Homoscedasticity is known as heteroscedasticity. We don’t need heteroscedasticity in data for linear regression. In other words, prior assumptions for linear regression is homoscedasticity exists in data.
Why do we need homoscedasticity For Linear Regression?
This is required for linear regression to ensure the reliability of estimated parameters and validity of statistical tests in linear regression.
How to check for Hetero-Scedasticity
We can check for heteroscedasticity in data using the following tests:
- Error vs Predicted value plot.
- Breusch-Pagan / Cook – Weisberg Test
- White General Test
Normally Distributed Prediction Error
Do we want our dependent and independent variables to be normally distributed for linear regression?
The answer is no.
Prior assumptions for linear regression is the prediction error is normally distributed. In other words prediction error should follow normal distribution with mean equal to 0.
Why we need to ensure the normal distribution of prediction error
If this assumption is true, we can do statistical significance or hypothesis testing, and calculate confidence interval on error data.
FAQ on Assumptions of Linear Regression
No, it does not matter if independent variables are normally distributed or they are not.
No, it does not matter if dependent variables are normally distributed or they are not.
